CF528D Fuzzy Search (生成函数+FFT)

题目传送门

题目大意：给你两个只包含A,G,C,T的字符串$S$,$T$，$S$长$T$短，按照如下图方式匹配 解释不明白直接上图

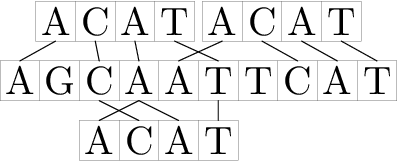
能容错的距离不超过$K$，求能$T$被匹配上的次数

$S$串同一个位置可以被$T$的不同位置匹配多次

对4种字符分别处理，假设我们现在只讨论字符A

对于字符串AGCAATTCAT，字符A的生成函数就是1001100010

题目要求距离不超过K就能匹配，把周围距离不超过$K$的位置都变成1，形成一个新串$S'$

$S$  1001100010

$S'$ 1111110111

只要$T$和$S'$的某个子串匹配时，子串中1的个数 不少于 $T$串中1的个数，就表明$T$串能被匹配上

把$T$串反转，再进行卷积，每一位都分4钟情况讨论即可

 #include <cmath>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #define N1 (1<<19)
 #define il inline
 #define dd double
 #define ld long double
 #define ll long long
 using namespace std;

 int gint()
 {
     int ret=,fh=;char c=getchar();
     while(c<''||c>''){if(c=='-')fh=-;c=getchar();}
     while(c>=''&&c<=''){ret=ret*+c-'';c=getchar();}
     return ret*fh;
 }
 int idx(char c)
 {
     if(c=='A') return ;
     if(c=='C') return ;
     if(c=='G') return ;
     if(c=='T') return ;
 }
 const int inf=0x3f3f3f3f;

 namespace FFT{

 const dd pi=acos(-);
 struct cp{
 dd x,y;
 friend cp operator + (const cp &s1,const cp &s2){ return (cp){s1.x+s2.x,s1.y+s2.y}; }
 friend cp operator - (const cp &s1,const cp &s2){ return (cp){s1.x-s2.x,s1.y-s2.y}; }
 friend cp operator * (const cp &s1,const cp &s2){ return (cp){s1.x*s2.x-s1.y*s2.y,s1.y*s2.x+s1.x*s2.y}; }
 }a[N1],b[N1],c[N1];
 int r[N1];
 void FFT(cp *s,int len,int type)
 {
     int i,j,k; cp wn,w,t;
     for(i=;i<len;i++) if(i<r[i]) swap(s[i],s[r[i]]);
     for(k=;k<=len;k<<=)
     {
         wn=(cp){cos(2.0*type*pi/k),sin(2.0*type*pi/k)};
         for(i=;i<len;i+=k)
         {
             w=(cp){,};
             for(j=;j<(k>>);j++,w=w*wn)
             {
                 t=w*s[i+j+(k>>)];
                 s[i+j+(k>>)]=s[i+j]-t;
                 s[i+j]=s[i+j]+t;
             }
         }
     }
 }
 void Main(int len,int L)
 {
     int i;
     for(i=;i<len;i++) r[i]=(r[i>>]>>)|((i&)<<(L-));
     FFT(a,len,); FFT(b,len,);
     for(i=;i<len;i++) c[i]=a[i]*b[i];
     FFT(c,len,-);
     for(i=;i<len;i++) c[i].x/=len;
 }
 void init()
 {
     memset(a,,sizeof(a));
     memset(b,,sizeof(b));
 }

 };
 using FFT::a; using FFT::b; using FFT::c;

 int s[N1],t[N1],nt[N1],n,m,K,len,L;
 char S[N1],T[N1];
 void solve(int p)
 {
     FFT::init();
     int i,j,k,num=;
     for(i=,k=;i<n;i++) if(s[i]==p)
         for(k=max(k,i-K);k<=min(n,i+K);k++) a[k].x=;
     for(i=n-,k=n-;i;i--) if(s[i]==p)
         for(k=min(k,i+K);k>=max(,i-K);k--) a[k].x=;
     for(i=;i<m;i++) if(t[i]==p) b[m-i-].x=,num++;
     FFT::Main(len,L);
     for(i=;i<n;i++) if((int)(c[i].x+0.1)<num) nt[i]=;
 }

 int main()
 {
     int i,j,ans=;
     scanf("%d%d%d",&n,&m,&K);
     scanf("%s",S); scanf("%s",T);
     for(i=;i<n;i++) s[i]=idx(S[i]);
     for(i=;i<m;i++) t[i]=idx(T[i]);
     for(len=,L=;len<(n+m-);len<<=,L++);
     solve();
     solve();
     solve();
     solve();
     for(i=;i<n;i++) if(!nt[i]) ans++;
     printf("%d\n",ans);
     return ;

 }