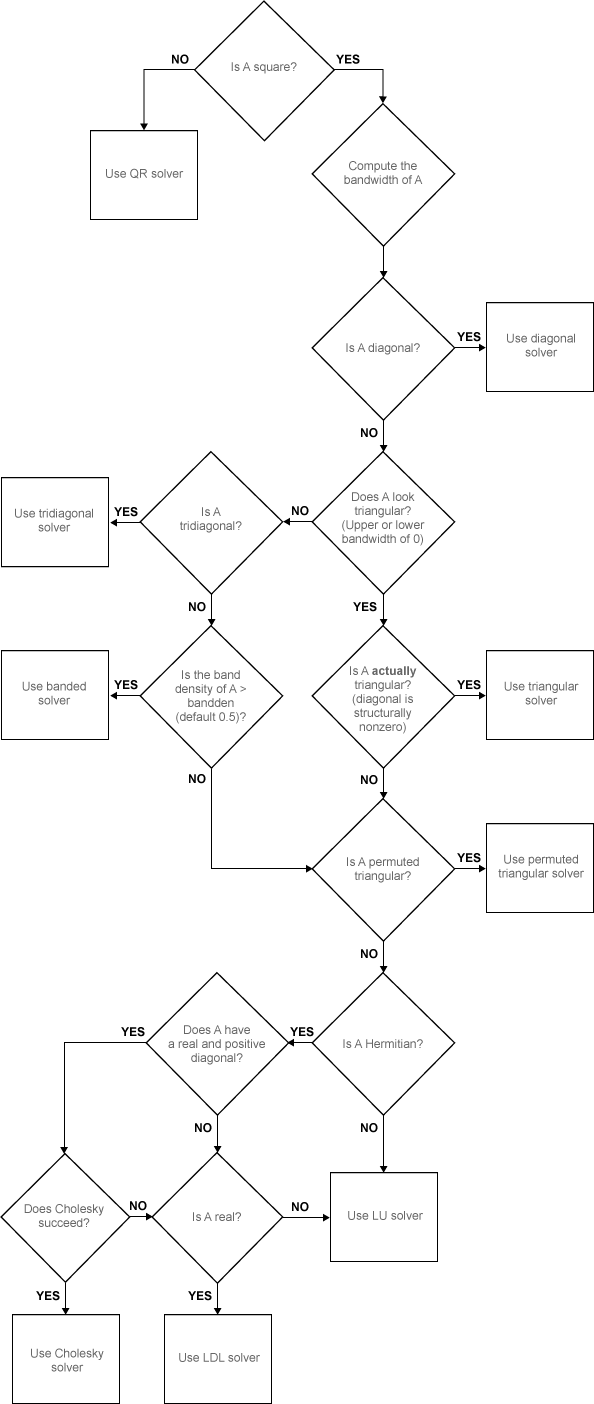
matlab 求解 Ax=B 时所用算法
x = A\B;
x = mldivide(A, B);matlab 在这里的求解与严格的数学意义是不同的,
- 如果 A 接近奇异,matlab 仍会给出合理的结果,但也会提示警告信息;
- 如果 A 为方阵,如果解存在的话,x = A\B 的解就是 Ax=B(代入就会成立)
- 如果 A 不为方阵,返回的是 Ax=B 的最小二乘解;
1. A 和 B 是 full 型矩阵(一般的矩阵)
2. A 为 sparse 型矩阵
matlab 求解 Ax=B 时所用算法的更多相关文章
- 文本主题模型之LDA(三) LDA求解之变分推断EM算法
文本主题模型之LDA(一) LDA基础 文本主题模型之LDA(二) LDA求解之Gibbs采样算法 文本主题模型之LDA(三) LDA求解之变分推断EM算法 本文是LDA主题模型的第三篇,读这一篇之前 ...
- yalmip + lpsolve + matlab 求解混合整数线性规划问题(MIP/MILP)
最近建立了一个网络流模型,是一个混合整数线性规划问题(模型中既有连续变量,又有整型变量).当要求解此模型的时候,发现matlab优化工具箱竟没有自带的可以求解这类问题的算法(只有bintprog求解器 ...
- matlab 求解线性规划问题
线性规划 LP(Linear programming,线性规划)是一种优化方法,在优化问题中目标函数和约束函数均为向量变量的线性函数,LP问题可描述为: minf(x):待最小化的目标函数(如果问题本 ...
- fslove - Matlab求解多元多次方程组
fslove - Matlab求解多元多次方程组 简介: 之前看到网上的一些资料良莠不齐,各种转载之类的,根本无法解决实际问题,所以我打算把自己的学到的总结一下,以实例出发讲解fsolve. 示例如下 ...
- 求解Ax=b
一 线性方程组 Ax=b 的解释 线性方程组 Ax=b,其中矩阵 A 尺寸为 m*n, 当 A 为方正时,可使用消元法判断解是否存在并求解.当 A 为长方形矩阵时,同样可使用消元法判断解存在情况并求解 ...
- Matlab 语谱图(时频图)绘制与分析
Matlab 语谱图(时频图)绘制与分析 语谱图:先将语音信号作傅里叶变换,然后以横轴为时间,纵轴为频率,用颜色表示幅值即可绘制出语谱图.在一幅图中表示信号的频率.幅度随时间的变化,故也称" ...
- 用Matlab求解微分方程
用Matlab求解微分方程 解微分方程有两种解,一种是解析解,一种是数值解,这两种分别对应不同的解法 解析解 利用dsolve函数进行求解 syms x; s = dsolve('eq1,eq2,.. ...
- 使用matlab用优化后的梯度下降法求解达最小值时参数
matlab可以用 -Conjugate gradient -BFGS -L-BFGS 等优化后的梯度方法来求解优化问题.当feature过多时,最小二乘计算复杂度过高(O(n**3)),此时 这一些 ...
- [Matlab]求解线性方程组
转自:http://silencethinking.blog.163.com/blog/static/911490562008928105813169/ AX=B或XA=B在MATLAB中,求解线性方 ...
随机推荐
- Android JAVA中的时间大小比较
import java.text.DateFormat; import java.text.ParseException; import java.text.SimpleDateFormat; imp ...
- linux下的多线程,pthread_create函数
pthread_create是UNIX环境创建线程函数 头文件 #include<pthread.h> 函数声明 int pthread_create(pthread_t*restrict ...
- 基于 Android NDK 的学习之旅-----JNI LOG 打印
程序都是调出来的. 下面我介绍下JNI层的log打印方法的使用,类似与Android sdk提供的log 1.Android 应用层 MainActivity.java 主要功能代码 a) ...
- mui常用功能链接地址
1.下拉刷新mui.pullToRefresh插件http://ask.dcloud.net.cn/article/12152.打包app权限列表http://ask.dcloud.net.cn/ar ...
- Codeforces Round #313 (Div. 2) 560C Gerald's Hexagon(脑洞)
C. Gerald's Hexagon time limit per test 2 seconds memory limit per test 256 megabytes input standard ...
- 《学习opencv》笔记——关于一些画图的函数
画图函数 (1)直线cvLine函数 其结构 void cvLine(//画直线 CvArr* array,//画布图像 CvPoint pt1,//起始点 CvPoint pt2,//终点 CvSc ...
- ITFriend创业败局(一):选择创业方向和寻找合伙人,创业失败的2个关键点
这次创业惨淡收场,最主要的原因是没有选择一个合适的创业方向,没有找到合适的创业合伙人. 首先要说到创业方向,因为不同的创业方向需要组建不同的创业团队.我个人比较偏好,软件.网络.互联网等有一 ...
- 手动安装MySQL8.0
首先跟大家唠一唠家常,随着MySQL迅速的更新,MySQL突飞猛进已经更新到了8.0版本,那么它和我们之前用的5.X版本有什么明显的区别那? 首先给大家看下MySQL5.X自带表的查询速度 之后献上M ...
- Java背景
Java语言是美国Sun公司(Stanford University Network),在1995年推出的高级编程语言 2009年Oracle甲骨文公司收购Sun公司
- 说下IEnumerable相关的
IEnumerable 我们每天都在使用foreach进行遍历,今天讨论下面三个常见的问题: 为什么在foreach中不能修改item的值 要实现foreach需要满足什么条件 为什么Linq to ...