【机器学习】Apriori算法——原理及代码实现（Python版）

Apriopri算法

Apriori算法在数据挖掘中应用较为广泛，常用来挖掘属性与结果之间的相关程度。对于这种寻找数据内部关联关系的做法，我们称之为：关联分析或者关联规则学习。而Apriori算法就是其中非常著名的算法之一。关联分析，主要是通过算法在大规模数据集中寻找频繁项集和关联规则。

• 频繁项集：经常出现在一起的物品或者属性的集合
• 关联规则：物品或者属性之间存在的内在关系（统计学上的关系）

所以，我们常见的Apriori算法中的主要包含两大模块内容，一块是寻找频繁项集的函数模块，一块是探索关联规则的函数模块。

支持度与置信度

支持度与置信度是实现Apriori算法无法回避的两个概念，支持度用来寻找频繁项集，而置信度用来确定关联规则。具体用处，在后续原理章节，进行介绍。

• 支持度:频繁项集在全体数据样本中所占的比例
  support(X, Y) = P(X, Y) = \frac{number(X, Y)}{number(all\ sample)}support(X,Y)=P(X,Y)=number(all sample)number(X,Y)​
• 置信度：体现为一个数据出现后，另一个数据出现的概率，或者说数据的条件概率
  confidence(X \Rightarrow Y) = P(Y | X) = \frac{P(X,Y)}{P(X)} =\frac{number(X,Y)}{number(X)}confidence(X⇒Y)=P(Y∣X)=P(X)P(X,Y)​=number(X)number(X,Y)​

Apriori算法原理

以商品购买为例，假设一家商店，出售四种商品，分别为商品0，商品1，商品2，商品3。我们希望通过挖掘买家购买商品的订单数据，来进行商品之间的组合促销或者说是摆放位置。那么商品之间可能的组合如下图所示：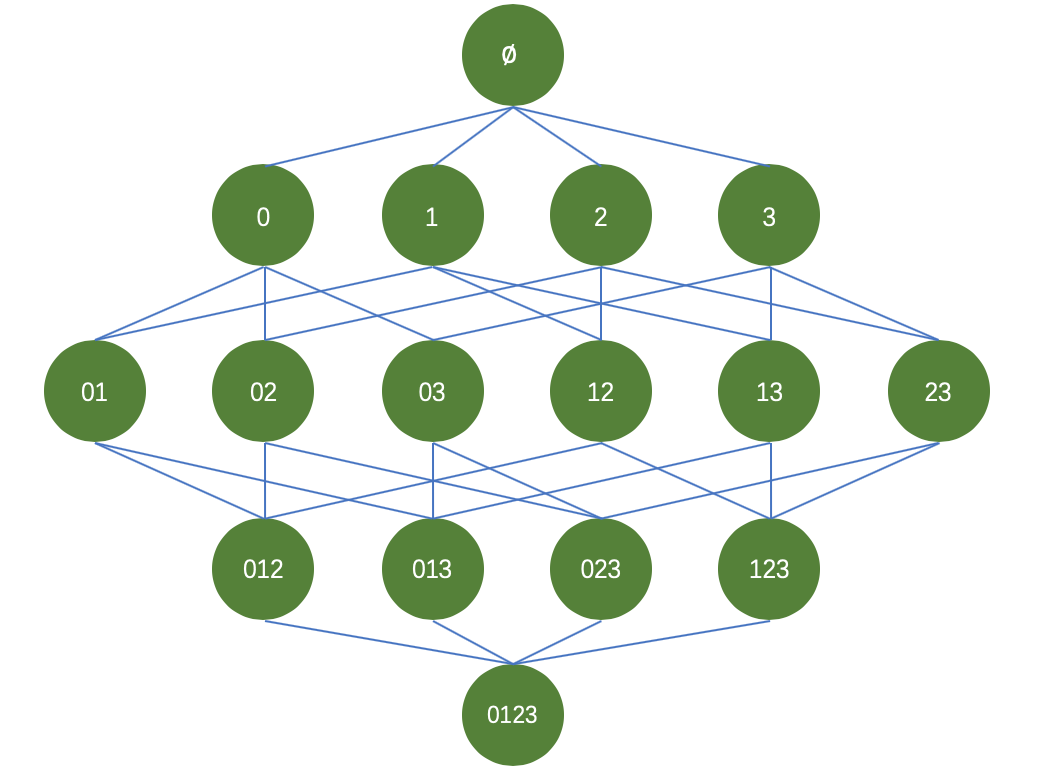

针对这些商品，我们的目标是：从大量购买数据中找到经常一起被购买的商品。在寻找频繁项集（即经常出现的商品组合）的过程中，我们采用支持度（support）来过滤商品组合，即频繁项集。针对四中商品，我们要在整体数据集上进行15次轮询，才可以统计出每个频繁项集的支持度。试想，如果数据量较大，且商品种类不止四中的情况下，难道依旧采用逐个轮询的方式进行统计吗？那么带来的运算量也是巨大的，并且随着商品种类的增加，频繁项集的组合种类也将变为2^N-12N−1种，随着种类的增加，那么带来的运算代价呈现指数型增加。为了解决这个问题，研究人员便在Apriori原理的基础上设计了Apriori算法。
Apriori原理如下：如果某个项集是频繁的，那么它的所有子集也是频繁的。反过来，如果一个项集是非频繁集，那么它的所有超集（包含该非频繁集的父集）也是非频繁的。
于是,可以将上图进行适当的优化，如下所示：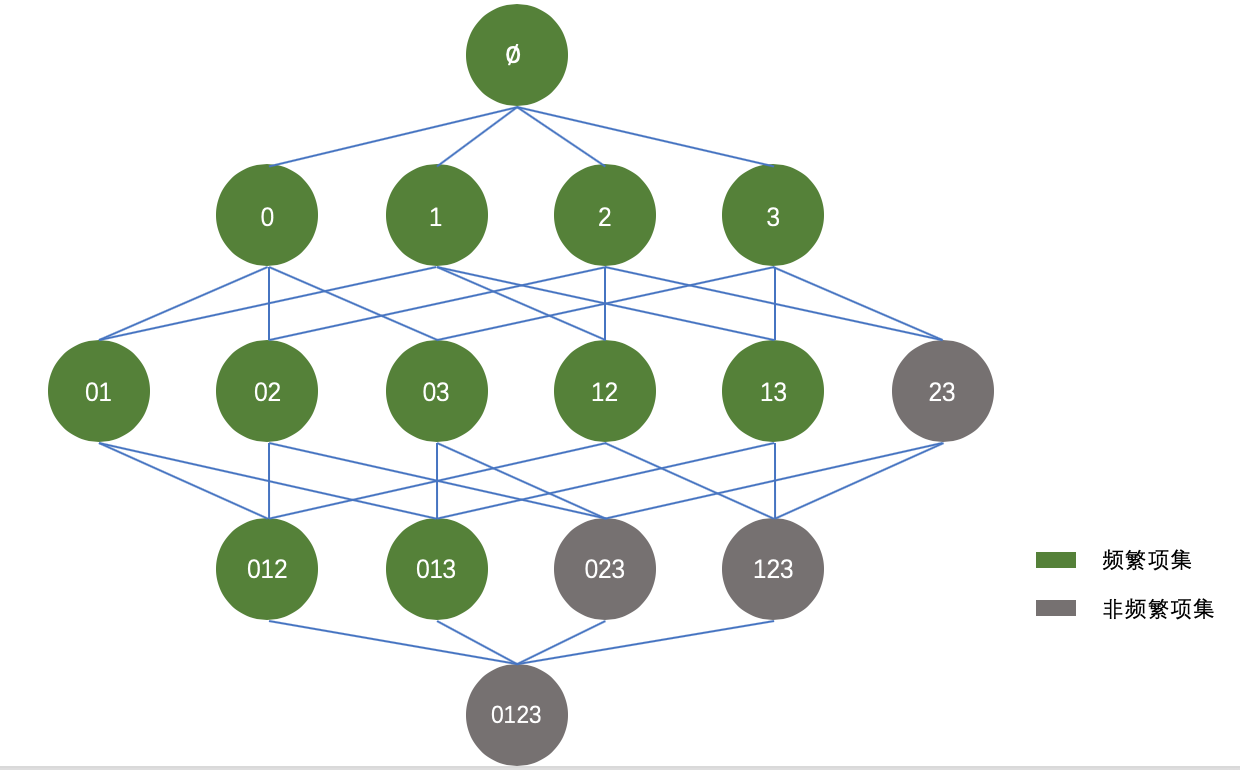

根据Apriori原理，我们知道阴影项集{2,3}是非频繁的，那么它的所有超集，也都是非频繁的，如上图灰色所示。在实际计算过程中，一旦计算出{2,3}的支持度不满足最小支持度，那么就不需要再计算{0,2,3}、{1,2,3}和{0,1,2,3}的支持度，因为它们也都是非频繁集。

Apriori算法实现

上面的部分也已经说了，Apriori算法主要有两部分组成：

• 发现频繁项集
• 找出关联规则

本部分将从两个方面来实现代码，具体如下所示：

发现频繁项集

def createC1(dataSet):
    C1=[]
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    return list(map(frozenset,C1))

def scanD(D,CK,minSupport):
    ssCnt = {}
    for tid in D:
        for can in CK:
            if can.issubset(tid):
                if not can in ssCnt:ssCnt[can]=1
                else:ssCnt[can]+=1
    numItems = float(len(D))
    retList = []
    supportData={}
    for key in ssCnt:
        support = ssCnt[key]/numItems
        if support>=minSupport:
            retList.insert(0,key)
        supportData[key]=support
    return retList,supportData
电动叉车
#频繁项集两两组合
def aprioriGen(Lk,k):
    retList=[]
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i+1,lenLk):
            L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
            L1.sort();L2.sort()
            if L1==L2:
                retList.append(Lk[i]|Lk[j])
    return retList

def apriori(dataSet,minSupport=0.5):
    C1=createC1(dataSet)
    D=list(map(set,dataSet))
    L1,supportData =scanD(D,C1,minSupport)
    L=[L1]
    k=2
    while(len(L[k-2])>0):
        CK = aprioriGen(L[k-2],k)
        Lk,supK = scanD(D,CK,minSupport)
        supportData.update(supK)
        L.append(Lk)
        k+=1
    return L,supportData

找出关联规则

#规则计算的主函数
def generateRules(L,supportData,minConf=0.7):
    bigRuleList = []
    for i in range(1,len(L)):
        for freqSet in L[i]:
            H1 = [frozenset([item]) for item in freqSet]
            if(i>1):
                rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
            else:
                calcConf(freqSet,H1,supportData,bigRuleList,minConf)
    return bigRuleList

def calcConf(freqSet,H,supportData,brl,minConf=0.7):
    prunedH=[]
    for conseq in H:
        conf = supportData[freqSet]/supportData[freqSet-conseq]
        if conf>=minConf:
            print (freqSet-conseq,'--->',conseq,'conf:',conf)
            brl.append((freqSet-conseq,conseq,conf))
            prunedH.append(conseq)
    return prunedH

def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):
    m = len(H[0])
    if (len(freqSet)>(m+1)):
        Hmp1 = aprioriGen(H,m+1)
        Hmp1 = calcConf(freqSet,Hmp1,supportData,brl,minConf)
        if(len(Hmp1)>1):
            rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)

整合整个代码如下所示：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Nov 30 16:38:01 2018

@author: lxh
"""

def loadDataSet():
    return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]

def createC1(dataSet):
    C1=[]
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    return list(map(frozenset,C1))

def scanD(D,CK,minSupport):
    ssCnt = {}
    for tid in D:
        for can in CK:
            if can.issubset(tid):
                if not can in ssCnt:ssCnt[can]=1
                else:ssCnt[can]+=1
    numItems = float(len(D))
    retList = []
    supportData={}
    for key in ssCnt:
        support = ssCnt[key]/numItems
        if support>=minSupport:
            retList.insert(0,key)
        supportData[key]=support
    return retList,supportData

#频繁项集两两组合
def aprioriGen(Lk,k):
    retList=[]
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i+1,lenLk):
            L1=list(Lk[i])[:k-2];L2=list(Lk[j])[:k-2]
            L1.sort();L2.sort()
            if L1==L2:
                retList.append(Lk[i]|Lk[j])
    return retList

def apriori(dataSet,minSupport=0.5):
    C1=createC1(dataSet)
    D=list(map(set,dataSet))
    L1,supportData =scanD(D,C1,minSupport)
    L=[L1]
    k=2
    while(len(L[k-2])>0):
        CK = aprioriGen(L[k-2],k)
        Lk,supK = scanD(D,CK,minSupport)
        supportData.update(supK)
        L.append(Lk)
        k+=1
    return L,supportData

#规则计算的主函数
def generateRules(L,supportData,minConf=0.7):
    bigRuleList = []
    for i in range(1,len(L)):
        for freqSet in L[i]:
            H1 = [frozenset([item]) for item in freqSet]
            if(i>1):
                rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
            else:
                calcConf(freqSet,H1,supportData,bigRuleList,minConf)
    return bigRuleList

def calcConf(freqSet,H,supportData,brl,minConf=0.7):
    prunedH=[]
    for conseq in H:
        conf = supportData[freqSet]/supportData[freqSet-conseq]
        if conf>=minConf:
            print (freqSet-conseq,'--->',conseq,'conf:',conf)
            brl.append((freqSet-conseq,conseq,conf))
            prunedH.append(conseq)
    return prunedH
def rulesFromConseq(freqSet,H,supportData,brl,minConf=0.7):
    m = len(H[0])
    if (len(freqSet)>(m+1)):
        Hmp1 = aprioriGen(H,m+1)
        Hmp1 = calcConf(freqSet,Hmp1,supportData,brl,minConf)
        if(len(Hmp1)>1):
            rulesFromConseq(freqSet,Hmp1,supportData,brl,minConf)

if __name__=='__main__':
    dataSet=loadDataSet()
    L,supportData=apriori(dataSet)
    rules = generateRules(L,supportData,minConf=0.7)

输出结果如下所示：