数学图形(1.47)贝塞尔(Bézier)曲线

贝塞尔曲线又称贝兹曲线或贝济埃曲线,是由法国数学家Pierre Bézier所发现，由此为计算机矢量图形学奠定了基础。它的主要意义在于无论是直线或曲线都能在数学上予以描述。

上一节讲的是高次方程曲线,其实贝塞尔曲线就是高次函数曲线.研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。涕淌为了向大家 介绍贝塞尔曲线的公式，也故意把问题的已知和所求颠倒了一下位置：如果已知一条曲线的参数方程，系数都已知，并且两个方程里都含有一个参数t，它的值介于 0、1之间，表现形式如下所示：

      x(t) = ax * t ^ 3 + bx * t ^ 2 + cx * t + x0
      y(t) = ay * t ^ 3 + by * t ^ 2 + cy * t + y0

由N个顶点控制的贝塞尔曲线,是N-1次的函数方程构成.

二次方贝塞尔曲线

二次方贝塞尔曲线的路径由给定点P₀、P₁、P₂的函数B（t）：

。

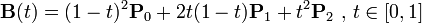三次方贝塞尔曲线

      P₀、P₁、P₂、P₃四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P₀走向P₁，并从P₂的方向来到P₃。一般不会经过P₁或P₂；这两个点只是在那里提供方向资讯。P₀和P₁之间的间距，决定了曲线在转而趋进P₃之前，走向P₂方向的“长度有多长”。

。

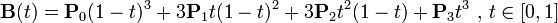阶贝塞尔曲线可如下推断:

给定点P₀、P₁、…、P_n，其贝塞尔曲线即

相关软件参见:数学图形可视化工具,使用自己定义语法的脚本代码生成数学图形.该软件免费开源.QQ交流群: 367752815

如下是我写的贝塞尔曲线的脚本代码与截图,代码中的控制顶点坐标为随机数生成.

二次方贝塞尔曲线:

vertices = 

t = from  to 

ax = rand2(-, )
ay = rand2(-, )
bx = rand2(-, )
by = rand2(-, )
cx = rand2(-, )
cy = rand2(-, )

a1 = (-t)*(-t)
a2 = *t*(-t)
a3 = t*t

x = a1*ax+a2*bx+a3*cx
y = a1*ay+a2*by+a3*cy

三次方贝塞尔曲线:

vertices = 

t = from  to 

ax = rand2(-, )
ay = rand2(-, )
bx = rand2(-, )
by = rand2(-, )
cx = rand2(-, )
cy = rand2(-, )
dx = rand2(-, )
dy = rand2(-, )

a1 = pow((-t),)
a2 = pow((-t),)**t
a3 = *t*t*(-t)
a4 = t*t*t

x = a1*ax+a2*bx+a3*cx+a4*dx;
y = a1*ay+a2*by+a3*cy+a4*dy; 

四次方贝塞尔曲线:

vertices = 

t = from  to 

ax = rand2(-, )
ay = rand2(-, )
bx = rand2(-, )
by = rand2(-, )
cx = rand2(-, )
cy = rand2(-, )
dx = rand2(-, )
dy = rand2(-, )
ex = rand2(-, )
ey = rand2(-, )

t2 = pow(t,)
t3 = pow(t,)
t4 = pow(t,)

w = -t
w2 = pow(w,)
w3 = pow(w,)
w4 = pow(w,)

a1 = w4
a2 = *w3*t
a3 = *w2*t2
a4 = *w*t3
a5 = t4

x = a1*ax+a2*bx+a3*cx+a4*dx+a5*ex;
y = a1*ay+a2*by+a3*cy+a4*dy+a5*ex; 

五次方贝塞尔曲线:

vertices = 

t = from  to 

ax = rand2(-, )
ay = rand2(-, )
bx = rand2(-, )
by = rand2(-, )
cx = rand2(-, )
cy = rand2(-, )
dx = rand2(-, )
dy = rand2(-, )
ex = rand2(-, )
ey = rand2(-, )
fx = rand2(-, )
fy = rand2(-, )

t2 = pow(t,)
t3 = pow(t,)
t4 = pow(t,)
t5 = pow(t,)

w = -t
w2 = pow(w,)
w3 = pow(w,)
w4 = pow(w,)
w5 = pow(w,)

a1 = w5
a2 = *w4*t
a3 = *w3*t2
a4 = *w2*t3
a5 = *w*t4
a6 = t5

x = a1*ax+a2*bx+a3*cx+a4*dx+a5*ex+a6*fx;
y = a1*ay+a2*by+a3*cy+a4*dy+a5*ex+a6*fx;