Educational Codeforces Round 38 (Rated for Div. 2) C

C. Constructing Tests

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's denote a m-free matrix as a binary (that is, consisting of only 1's and 0's) matrix such that every square submatrix of size m × m of this matrix contains at least one zero.

Consider the following problem:

You are given two integers n and m. You have to construct an m-free square matrix of size n × n such that the number of 1's in this matrix is maximum possible. Print the maximum possible number of 1's in such matrix.

You don't have to solve this problem. Instead, you have to construct a few tests for it.

You will be given t numbers x1, x2, ..., xt. For every 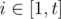, find two integers ni and mi (ni ≥ mi) such that the answer for the aforementioned problem is exactly xi if we set n = ni and m = mi.

Input

The first line contains one integer t (1 ≤ t ≤ 100) — the number of tests you have to construct.

Then t lines follow, i-th line containing one integer xi (0 ≤ xi ≤ 109).

Note that in hacks you have to set t = 1.

Output

For each test you have to construct, output two positive numbers ni and mi (1 ≤ mi ≤ ni ≤ 109) such that the maximum number of 1's in a mi-free ni × ni matrix is exactly xi. If there are multiple solutions, you may output any of them; and if this is impossible to construct a test, output a single integer  - 1.

Example

input

Copy

3
21
0
1

output

5 2
1 1
-1

思路

一个n*n的矩阵（由01组成）分成若干个m*m的矩阵，每个m*m的矩阵中0的个数不得小于1.那么每一行都至少有n/m个0，每一列也是至少n/m个0，

可以推出公式   x = n*n - (n/m)*(n/m)  分解可得  x = (n - n.m)*(n + n/m) 然后直接对于x因式分解 设 x = a*b ,a = (n-n/m),b = (n + n/m).然后暴力枚举a,b

由 a + b 可以得出 a + b = 2*n; n/m = sqrt(n*n - x); 则 m = n/sqrt(n*n - x).....根据枚举的ab,看能否求出符合条件的n , m，如果没有的话就输出-1。

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main()
{
    ll n,x;
    cin>>n;
    while(n--){
        cin>>x;
        ll flag = ;
        if(x==){ cout<<<<" "<<<<endl;continue;}
        for(ll i = ;i*i <= x;i++){
            if(x%i==){
                if((i+x/i)%==) continue;
                ll n1 = (i + x/i)/;
                ll m = n1*n1 - x;
                ll m1 = sqrt(m);
                if(m1*m1 != m||n1==||m1==) continue;
                if(n1*n1 - (n1/(n1/m1)*(n1/(n1/m1)))!=x) continue;
                cout<<n1<<" "<<n1/m1<<endl;
                flag = ;
                break;
            }
        }
        if(!flag) cout<<-<<endl;
    }
    return ;
}