Logistic Regression Algorithm

逻辑回归算法LR。

简介

逻辑回归是机器学习从统计学领域借鉴的另一种技术。它是二进制分类问题的首选方法(有两个类值的问题)。

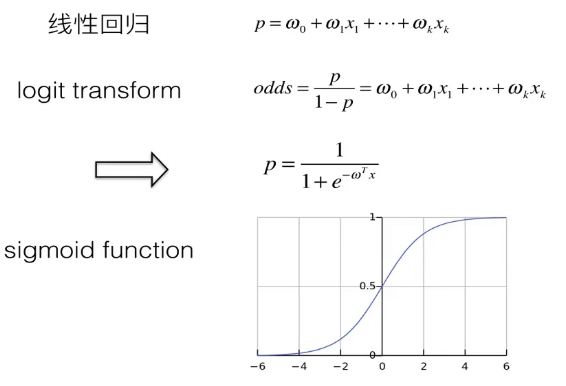
Logistic回归就像线性回归，目标是找到权重每个输入变量的系数值。

与线性回归不同的是，对输出的预测用一个叫做logistic函数的非线性函数来进行转换。

logistic函数看起来像一个大S，它将把任何值转换为0到1的范围。我们可以将一个规则应用到逻辑函数的输出中，将值的值设为0和1(例如，如果小于0.5，则输出1)并预测一个类值。

由于模型的学习方式，逻辑回归的预测也可以作为一个给定数据实例的概率，属于第0类或第1类。这对于需要为预测提供更多理由的问题很有用。

与线性回归一样，当删除与输出变量无关的属性和非常相似(相关)的属性时，逻辑回归的效果会更好。

这是一个快速学习和有效的二元分类问题的模型。

碰到二分类的机器学习问题，企业级应用多选择逻辑回归的原因：

数据的丰富性比模型的选择要重要
模型的数据吞吐能力（企业级应用具有大规模海量数据）
求解算法的并行化难度
模型的迭代速度
特征的自解释性即basecase控制

回归方法的核心就是为函数找到最合适的参数，使得函数的值和样本的值最接近。例如线性回归(Linear regression)就是对于函数f(x)=ax+b，找到最合适的a,b。

LR拟合的就不是线性函数了，它拟合的是一个概率学中的函数，f(x)的值这时候就反映了样本属于这个类的概率。

LR同样是很多分类算法的基础组件，它的好处是输出值自然地落在0到1之间，并且有概率意义。

因为LR本质上是一个线性的分类器，所以处理不好特征之间相关的情况。

虽然效果一般，却胜在模型清晰，背后的概率学经得住推敲。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。

优点：

　　实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低；

缺点：

　　容易欠拟合，分类精度可能不高

LR求解

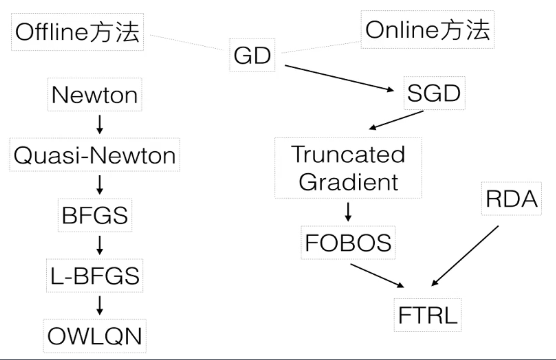
有很多种求解LR问题的方法，下面是一部分。主要分为离线和在线方法。

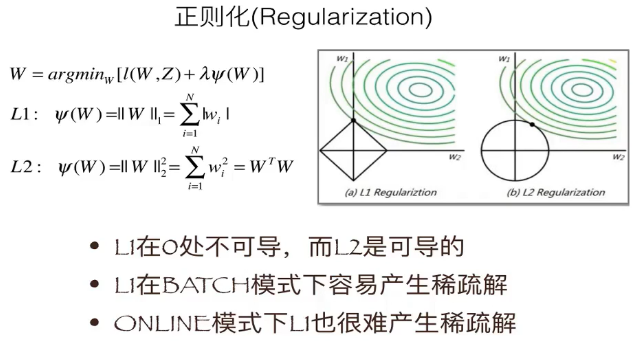
L1范数求解

用L1范数求解，但是L1范数不是处处可导的（一阶导在0处不可导），所以我们采用虚梯度来计算。

离线方法

最优步长搜索方法可以考虑line search方法。

关于two-loop，更多可参考2003年微软研究院的代码实现。

企业级应用主要考虑的是性能和精度的权衡。更看重数据的稀疏性。这也是采用L1范数的原因，因为L1范数具有稀疏性。

OFFLINE求解的假设：

将实际场景中的样本分为训练集和测试集，它们应该是近似同分布的。
模型中国选择的特征具有良好的泛化性。

Batch训练

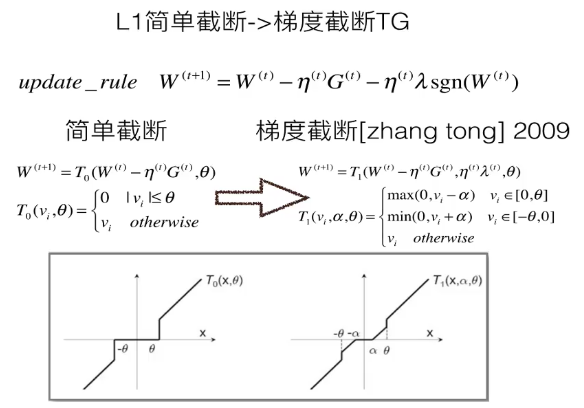
梯度截断——引入稀疏解

RDA 对偶平均，微软在2010年提出。

公式来自于作者在2014年提出。FTRL已经用于很多公司的online服务中。也算是online learning的一个标配。

online引入的问题：

sampling是否有收益
online训练的瓶颈
batch/online ensembling
online场景下特征如何调研