bzoj3504: [Cqoi2014]危桥

题意：给出一个图，有的边可以无限走，有的只能走两次（从一头到另一头为一次），给定两个起点以及对应的终点以及对应要走几个来回，求判断是否能完成。

先来一个NAIVE的建图：直接限制边建为容量1，无限制为INF，按照原图连，然后跑最大流就可以了。

可惜这样还不够，因为有可能有一部分流量不是对应的起点流过来的，即两条路有流量交换，这样就不一定可以满足题意了。

解决方法是：再跑一遍网络流，但是建图要改变一下，即将a路线的起点终点调换一下（当然b也可以），再接着跑，如果仍然满足则是真的有解。

证明看了网上的，都说的不太清楚，然后与ihopenot大爷讨论了下，有了一个证明（如果错了请指出）。

我们现在要证如果一开始的第一遍网络流跑出来满足条件并且第二遍也满足，则说明一定有真正满足题意的方案存在。

如果有交叉流，我们画一张图。

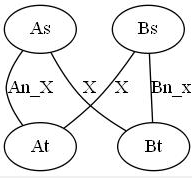
（因为使用的画图软件不能用减号，所以用下划线代替）其中As为起点，At为终点（B同理）

我们第二次建图后，如果能没有交叉流，那很好，直接说明有这种方案（因为倒过来是一样的嘛），但我们纠结的是，如果第二次仍然有交叉流怎么办？

我们画出来，发现，Bs到As有x的流量，第一张图又有As到Bt的x流量，那么这就是另一条x流量，与第一张图合起来不就是Bn吗，同理，A也是可以这样证明有满足条件且不交叉的流，那么就说明，我们如果两遍跑出来都满足，那就真的是有解的了。

送上代码

 #include<bits/stdc++.h>
 using namespace std;
 #define N 5005
 #define INF 1e9
 inline int read(){
     int x=,f=; char a=getchar();
     while(a>'' || a<'') {if(a=='-') f=-; a=getchar();}
     while(a>='' && a<='') x=x*+a-'',a=getchar();
     return x*f;
 }
 int n,d[N],head[N],cur[N],cnt,S,T,a1,a2,an,b1,b2,bn,ans;
 bool vis[N],g[][],b[][];
 queue<int>q;
 char st[][];
 struct edges{
     int to,cap,flow,next;
 }e[*N];
 inline void insert(int u,int v,int c){
     e[cnt]=(edges){v,c,,head[u]};head[u]=cnt++;
     e[cnt]=(edges){u,,,head[v]};head[v]=cnt++;
 }
 inline bool bfs(){
     memset(vis,,sizeof(vis));
     d[S]=; vis[S]=; q.push(S);
     while(!q.empty()){
         int x=q.front(); q.pop();
         for(int i=head[x];i>=;i=e[i].next)
             if(!vis[e[i].to] && e[i].cap>e[i].flow)
             d[e[i].to]=d[x]+,vis[e[i].to]=,q.push(e[i].to);
     }
     return vis[T];
 }
 int dfs(int x,int a){
     if(x==T || !a) return a;
     int f,flow=;
     for(int& i=cur[x];i>=;i=e[i].next){
         if(d[e[i].to]==d[x]+ && (f=dfs(e[i].to,min(a,e[i].cap-e[i].flow)))>)
         flow+=f,e[i].flow+=f,e[i^].flow-=f,a-=f;
         if(!a) break;
     }
     return flow;
 }
 inline int maxflow(){
     int flow=;
     while(bfs()){
         for(int i=S;i<=T;i++) cur[i]=head[i];
         flow+=dfs(S,INF);
     }
     return flow;
 }
 inline void build(){
     memset(head,-,sizeof(head)); cnt=;
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             if(g[i][j]) insert(i,j,INF);
             else if(b[i][j]) insert(i,j,);
 }
 int main(){
     S=; T=;
     while(scanf("%d",&n)!=EOF){
         memset(g,,sizeof(g));
         memset(b,,sizeof(b));
         a1=read()+; a2=read()+; an=read();
         b1=read()+; b2=read()+; bn=read();
         for(int i=;i<=n;i++) scanf("%s",st[i]+);
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++)
                 if(st[i][j]=='O') b[i][j]=;
                 else if(st[i][j]=='N') g[i][j]=;
         bool flag=;
         build(); insert(S,a1,an); insert(a2,T,an); insert(S,b1,bn); insert(b2,T,bn);
         if(maxflow()<an+bn) flag=;
         if(!flag){
             build(); insert(S,a2,an); insert(a1,T,an); insert(S,b1,bn); insert(b2,T,bn);
             if(maxflow()<an+bn) flag=;
         }
         if(flag) puts("No");
         else puts("Yes");
     }
     return ;
 }