Linear Algebra lecture6 note

Vector spaces and subspaces

Column space of A solving Ax=b

Null space of A

 

---

Vector space requirements v+w and cv are in the space

All combs cv+dw are in the space

向量空间对数乘和加法需要封闭

subspace of R^3:

Line( L) through zero vector  is a subspace of R^3

Plane( P) through zero vector is a subspace of R^3

then we got 2 subspaces: P and L

P∪L means all vectors in P or L or both, this is not a subspace, 原因在于对加法不封闭，加和后所得的可能既不在P上，也不在L上

P∩L means all vectors in both P and L, this is a subspace, 交点为zero

 

---

Column space of A（列空间），记作C（A）

example:

     is a subspace of R^4, 记作 C ( A)

思考：Does Ax=b have a solution for every b? Which b’s allow this system to be solved?

回答：No. 4 equations, 3 unknowns, we can solve Ax=b exactly when b is in C( A)

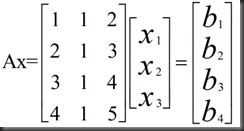
接下来考虑nullspace of A: all solutions to Ax=0

now write some solutions, such as

观察规律可总结出一般形式

Check the solution to Ax=0 always give a subspace

If Av=0 and Aw=0, then A(v+w)=0, then A(12v)=0,即对加法和数乘都封闭

 

another example：

解中不包含zero vector，故不构成space，那么它的解是什么样的呢？

是不穿过原点的平面或直线

summary：

subspace：1、combination of several vectors

                       2、从方程组中通过让x满足特定条件