CodeForces 907F Power Tower(扩展欧拉定理)

Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is usually made of power-charged rocks. It is built with the help of rare magic by levitating the current top of tower and adding rocks at its bottom. If top, which is built from k - 1 rocks, possesses power p and we want to add the rock charged with power w_k then value of power of a new tower will be {w_k}^p.

Rocks are added from the last to the first. That is for sequence w₁, ..., w_m value of power will be

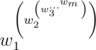
After tower is built, its power may be extremely large. But still priests want to get some information about it, namely they want to know a number called cumulative power which is the true value of power taken modulo m. Priests have n rocks numbered from 1 to n. They ask you to calculate which value of cumulative power will the tower possess if they will build it from rocks numbered l, l + 1, ..., r.

Input

First line of input contains two integers n (1 ≤ n ≤ 10⁵) and m (1 ≤ m ≤ 10⁹).

Second line of input contains n integers w_k (1 ≤ w_k ≤ 10⁹) which is the power of rocks that priests have.

Third line of input contains single integer q (1 ≤ q ≤ 10⁵) which is amount of queries from priests to you.

k^th of next q lines contains two integers l_k and r_k (1 ≤ l_k ≤ r_k ≤ n).

Output

Output q integers. k-th of them must be the amount of cumulative power the tower will have if is built from rocks l_k, l_k + 1, ..., r_k.

Example

Input

6 1000000000
1 2 2 3 3 3
8
1 1
1 6
2 2
2 3
2 4
4 4
4 5
4 6

Output

1
1
2
4
256
3
27
597484987

Note

3²⁷ = 7625597484987

题意:给出一个数字序列和一个固定的模数mod,给出q个询问,每次询问f(l,r)

f(l,r) =a[l]^(a[l+1]^(a[l+2]^(a[l+3]^(...^a[r])))%mod (^是幂次的意思)

题解:扩展欧拉定理告诉我们

然后我们尝试展开a^b^c

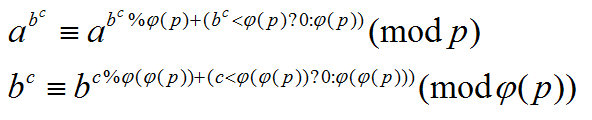
再往下也是一样的,我们可以先预处理出phi[p],phi[phi[p]]……

大概要处理几层呢?logn层,为什么呢?

假设phi[now]=1了

那么之上不管多少层

x=1,2,3,4,5……

这些数模一都是一

所以就成了欧拉函数的衰变速度(我瞎糊的名词,意思是经过几次phi,p会变成1)

这个复杂度是logn的,我们可以对这进行一发dfs,加上快速幂的logn复杂度,总复杂度是loglogn的,值得一提的是,快速幂中也要改成扩展欧拉定理的形式,否则小心炸掉~

顺便可以研究一下这道题是怎么被博主伪装成线段树的

U23882 天真♂哲学家♂树(Naive Philosopher Tree)

代码如下:

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int a[],phi[],n,m,mod;

int get(int x)
{
    int ans=x;
    for(int i=;i*i<=x;i++)
    {
        if(x%i==)
        {
            ans=ans/i*(i-);
            while(x%i==)
            {
                x/=i;
            }
        }
    }
    if(x!=)
    {
        ans=ans/x*(x-);
    }
    return ans;
}

int gg(long long x,int p)
{
    return x>=p?x%p+p:x;
}

int kasumi(int a,int b,int p)
{
    int ans=;
    while(b)
    {
        if(b&)
        {
            ans=gg(1ll*ans*a,p);
        }
        a=gg(1ll*a*a,p);
        b>>=;
    }
    return ans;
}

int dfs(int l,int r,int i)
{
    if(l==r||phi[i]==)
    {
        return gg(a[l],phi[i]);
    }
    return kasumi(a[l],dfs(l+,r,i+),phi[i]);
}

int main()
{
    scanf("%d%d",&n,&mod);
    phi[]=mod;
    for(int i=;i<=;i++)
    {
        phi[i]=get(phi[i-]);
    }
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    scanf("%d",&m);
    for(int i=;i<=m;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",dfs(l,r,)%mod);
    }
    return ;
}