Machine Learning系列--EM算法理解与推导

EM算法，全称Expectation Maximization Algorithm，译作最大期望化算法或期望最大算法，是机器学习十大算法之一，吴军博士在《数学之美》书中称其为“上帝视角”算法，其重要性可见一斑。

EM算法是一种迭代算法，用于含有隐变量（hidden variable）的概率参数模型的最大似然估计或极大后验概率估计。它与极大似然估计的区别就是它在迭代过程中依赖极大似然估计方法。极大似然估计是在模型已知的情况下,求解模型的参数$\theta$,让抽样出现的概率最大。类似于求解一元方程，所以极大似然估计参数值是稳定的。而对于EM算法，由于有隐藏变量（可视为多元参数）的存在，所以往往初始参数设置的不同会导致最后收敛的结果不同，使得陷入局部最优解，而非全局最优解)。但在隐藏变量$X$未知的情况下，通过计算其数学期望（E步），再利用极大似然求解（M步），为问题的近似解决提供了可能。

一、Jensen不等式

在完善EM算法之前，首先来了解下Jensen不等式，因为在EM算法的推导过程中会用到。

Jensen不等式在高中时我们就接触过，文字描述如下：

如果$f(X)$是凸函数，$X$是随机变量，则$E[f(X)] \ge f(E[X])$，特别地，如果$f$是严格凸函数，$E[f(X)] \ge f(E[X])$，那么当且仅当$p(x=E[X])=1$时（也就是说$X$是常量），$E[f(x)]=f(E[X])$；
如果$f(X)$是凹函数，$X$是随机变量，则$f(E[X]) \le E[f(X)]$，当$f(X)$是（严格）凹函数当且仅当$-f(X)$是（严格）凸函数。

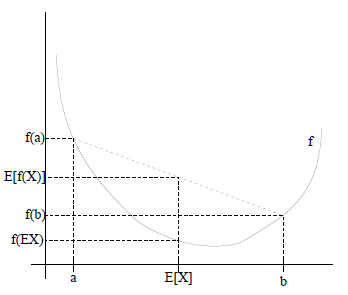
Jensen不等式图形化表达

二、 EM算法推导

给定$m$个训练样本（或观测变量数据）${x^{(1)},x^{(2)},\ldots,x^{(m)}}$，$n$个隐变量${z^{(1)},z^{(2)},\ldots,z^{(n)}}$，联合分布$P(X,Z|\theta)$，条件分布$P(Z|X, \theta)$。假设样本间相互独立，我们想要拟合模型$P(X,Z|\theta)$得到模型参数$\theta$。

首先，根据极大似然求解步骤（对似然函数取对数，求导数，令导数为0，得到似然方程，解似然方程后，得到的参数即为所求），我们列出如下似然函数：

\begin{align*}
l\left( \theta \right) &= \sum\limits_{i = 1}^m {\log p\left( {x;\theta } \right)} \\
&= \sum\limits_{i = 1}^m {\log \sum\nolimits_z {p\left( {x,z;\theta } \right).} }
\end{align*}

上式中，第一步是对极大似然函数取对数，第二步是对每个样本实例的每个可能的类别$z$求联合分布概率之和。然而，求这个参数$\theta$很困难，因为存在一个隐含随机变量$z$。如果能通过计算$z$的数学期望来估计$z$，代入式中后，再使用极大似然估计来解$\theta$就水到渠成。这也就是EM算法所要解决的问题场景。

接下来，我们引入$Q_i$函数，$Q_i$函数表示样本实例隐含变量z的某种分布，且$Q_i$满足条件$\sum_zQ_i(z)=1,Q_i(z)>=0$,如果$Q_i$是连续性的，则$Q_i$表示概率密度函数，需要将求和符号换成积分符号。

值得注意的是，此处的$Q_i$函数是分布，不是《统计学习方法》书中的期望$Q$函数（在给定观测数据$X$和当前参数$\theta^{(i)}$下对未观测数据$Z$的条件概率分布$P(Z|X, \theta)$的数学期望）。计算分布函数$Q_i$和计算期望$Q$函数是等价的。

计算$Q_i$函数或$Q$函数的过程就是E步，我们接着上面的推导过程继续：

\begin{align*}
\sum\limits_i {\log p\left( {{x^{\left( i \right)}};\theta } \right)} &= \sum\limits_i {\log \sum\limits_{{z^{\left( i \right)}}} {p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)} } \\
&= \sum\limits_i {\log \sum\limits_{{z^{\left( i \right)}}} {{Q_i}\left( {{z^{\left( i \right)}}} \right)\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} } \\
&\ge \sum\limits_i {\sum\limits_{{z^{\left( i \right)}}} {{Q_i}\left( {{z^{\left( i \right)}}} \right)\log \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} }
\end{align*}

上式中，第一步根据联合概率密度下某个变量的边缘密度函数求解展开，但式中求解隐变量$z$困难，于是第二步引入$Q_{i}(z^{(i)})$使分子分母平衡。

第三步根据Jensen不等式，已知$log(x)$的二阶导数为$-\frac{1}{x^2}$，属于凹函数，所以有$f(E[X])>=E[f(x)]$。

第三步具体的推导过程是：

a. 根据《概率论》中的期望公式$E(x)=\sum g(x)*p(x)$，$Y=g(x)$为随机变量$x$的函数，$P(X=x_k)=p_k$为分布律。将$Q_{i}(z^{(i)})$看成分布律$p(x)$，$\frac{p(x^{i},z^{(i)};\theta)}{Q_i(z^{(i)})}$看成值域$g(x)$，有：
\begin{align*}
E\left( {\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} \right) = \sum\limits_{{z^{\left( i \right)}}} {{Q_i}\left( {{z^{\left( i \right)}}} \right)\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}}
\end{align*}

b. 根据Jensen不等式的性质，对于凹函数有：
\begin{align*}
f\left( {{E_{{z^{\left( i \right)}} \sim {Q_i}}}\left( {\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} \right)} \right) \ge {E_{{z^{\left( i \right)}} \sim {Q_i}}}\left( {f\left( {\frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{{Q_i}\left( {{z^{\left( i \right)}}} \right)}}} \right)} \right)
\end{align*}

因此便得到了第三步。上述推导过程最后变为$L(\theta)>=J(z,Q)$的形式（$z$为隐含变量），那么我们可以通过不断的最大化$J$的下界，来使得$L(\theta)$不断提高，最终达到它的最大值。

接下来，我们需要推导出$Q_{i}(z^{(i)})$的具体表达形式，即隐变量$z$的分布或期望。

$Q_i$函数是隐变量$z$的分布，那么有下式：

\begin{align*}
{Q_i}\left( {{z^{\left( i \right)}}} \right) &= \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{\sum\nolimits_z {p\left( {{x^{\left( i \right)}},z;\theta } \right)} }}\\
&= \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};\theta } \right)}}{{p\left( {{x^{\left( i \right)}};\theta } \right)}}\\
&= p\left( {{z^{\left( i \right)}}|{x^{\left( i \right)}};\theta } \right)
\end{align*}

$Q$函数是隐变量$z$的期望，那么有下式：
$$ Q\left( \theta \right) = {E_Z}\left[ {\log P\left( {X,Z|\theta } \right)|X,{\theta ^{\left( i \right)}}} \right] $$

至此，我们推出了$Q(z)$的计算公式(后验概率或条件概率)。此步就是EM算法的E步，目的是建立$L(\theta)$的下界。

接下来的M步，目的是在给定$Q(z)$后，调整$\theta$，从而极大化$L(\theta)$的下界$J$（在固定$Q(z)$后，下界还可以调整的更大）。

到此，可以说是完美的展现了EM算法的E-step & M-step，完整的流程如下：

(1). 选择参数的初值$\theta^{(0)}$，开始迭代；
(2). E步：记$\theta^{(i)}$为第$i$次迭代参数$\theta$的估计值，在第$i+1$次迭代的E步，计算隐变量期望$Q$函数：
\begin{align*}
Q\left( \theta \right) &= {E_Z}\left[ {\log P\left( {X,Z|\theta } \right)|X,{\theta ^{\left( i \right)}}} \right]\\
&= \sum\limits_Z {\log P} \left( {X,Z|\theta } \right)P\left( {Z|X,{\theta ^{\left( i \right)}}} \right)
\end{align*}
这里，$P\left( {Z|X,{\theta ^{\left( i \right)}}} \right)$是在给定观测数据$X$和当前的参数估计$\theta^{(i)}$下隐变量$Z$的条件概率分布，也就是$Q_i$函数。
(3). M步: 求使$Q\left( \theta \right)$极大化的$\theta$，确定第$i+1$次迭代的参数估计值$\theta^{(i+1)}$.
$$ \theta^{(i+1)} = arg \mathop {max }\limits_Q Q\left( \theta \right) $$
(4). 重复第(2)和第(3)步，直到收敛。

三、 EM算法的收敛性

如何保证EM最终是收敛的呢？

由极大似然估计的迭代过程：

\begin{align*}
l\left( {{\theta ^{\left( {t + 1} \right)}}} \right) &\ge \sum\limits_i {\sum\limits_{{z^{\left( i \right)}}} {{Q_i}^{\left( t \right)}\left( {{z^{\left( i \right)}}} \right)\log \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};{\theta ^{\left( {t + 1} \right)}}} \right)}}{{{Q_i}^{\left( t \right)}\left( {{z^{\left( i \right)}}} \right)}}} } \\
&\ge \sum\limits_i {\sum\limits_{{z^{\left( i \right)}}} {{Q_i}^{\left( t \right)}\left( {{z^{\left( i \right)}}} \right)\log \frac{{p\left( {{x^{\left( i \right)}},{z^{\left( i \right)}};{\theta ^{\left( t \right)}}} \right)}}{{{Q_i}^{\left( t \right)}\left( {{z^{\left( i \right)}}} \right)}}} } \\
&= l\left( {{\theta ^{\left( t \right)}}} \right)
\end{align*}

这样就证明了$l(\theta)$会单调增加。如果要判断收敛情况，可以这样来做：一种收敛方法是$l(\theta)$不再变化，还有一种就是变化幅度很小,即根据$l(\theta)^{(t+1)}-l(\theta)^{(t)}$的值来决定。

EM算法类似于坐标上升法（coordinate ascent）：E步:计算隐变量期望$Q$；M步：将期望$Q$代入极大似然估计中，估算$\theta$；交替将极值推向最大。

参考博文：