P3379 【模板】最近公共祖先（LCA）

P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1：

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出样例#1：

4
4
1
4
4

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

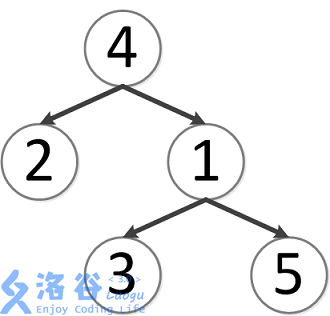
第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

 #include<iostream>
 #include<cstdio>

 using namespace std;

 const int N = ;

 int n,m,root,ans,cnt;
 int head[N];
 int deth[N];
 int f[N][];
 bool vis[N];
 struct Edge{
     int to,nxt;
 }e[N<<];

 int Read()
 {
     int x=,f=;
     char c=getchar();
     while(c>''||c<'') {if(c=='-') f=-;c=getchar();}
     while(c>=''&&c<='') {x=x*+c-''; c=getchar();}
     return x*f;
 }

 void add(int a,int b)
 {
     ++cnt;
     e[cnt].to = b;
     e[cnt].nxt = head[a];
     head[a] = cnt;
 }

 void dfs(int a)
 {
     vis[a] = true;
     for(int i=;i<=;i++)
     {
         if(deth[a] < (<<i)) break;
         f[a][i] = f[f[a][i-]][i-];
     }
     for(int i=head[a];i;i=e[i].nxt)
     {
         int now = e[i].to;
         if(!vis[now])
         {
             deth[now] = deth[a]+;
             f[now][]=a;
             dfs(now);
         }
     }
 }

 int lca(int u,int v)
 {
     if(deth[u] < deth[v])swap(u,v);
     int d = deth[u] - deth[v];
     for (int i=; i<; i++)    //值得注意的是，这里需要从零枚举
     {
         if ( (<<i) & d)//一个判断，模拟一下就会很清晰
             u = f[u][i];
     }
     if (u==v) return u;
     for (int i=; i>=; i--)
     {
         if (f[u][i]!=f[v][i])     //跳2^j步不一样，就跳，否则不跳
         {
             u = f[u][i];
             v = f[v][i];
         }
     }
     u = f[u][];        //上述过程做完，两点都在LCA下一层，所以走一步即可
     return u;
 }

 int main()
 {
     int x,y;
     n=Read();
     m=Read();
     root=Read();
     for(int i=;i<n;i++)
     {
         x=Read();
         y=Read();
         add(x,y);
         add(y,x);
     }
     deth[root] = ;
     dfs(root);
     while(m--)
     {
         x=Read();
         y=Read();
         printf("%d\n",lca(x,y));
     }
     return ;
 }