LeetCode: 60. Permutation Sequence（Medium）

1. 原题链接

https://leetcode.com/problems/permutation-sequence/description/

2. 题目要求

给出整数 n和 k ，k代表从1到n的整数所有排列序列中的第k个序列，返回String类型的第k个序列

3. 解题思路

首先我们要知道这个序列是按照什么规律排列下去的，假如此时n=4，k= 21，n=4时所有的排列如下：

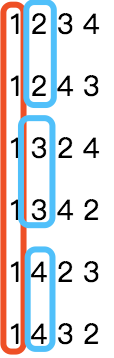
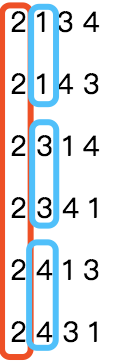
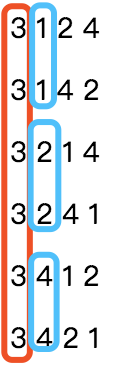
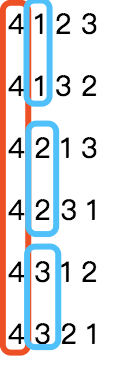
可以看出 n=4 时，一共有 4!=24种排列组合。

每一个数字开头各有 6 种排列组合，因此我们可以把同一数字开头的排列看作同一组，一共 4 组。

我们进一步探寻排列的规律。

（1） 第一步： 确定第一个数字

k=21，也就是要我们找到第19个排列组合，这个组合的第一个数字我们使用  (21-1)/(4-1)! = 3 ，3对应未使用数字中的第四位数字“4”，所以第一位数字为4。

将 4 从未使用数字中去除，还剩：1 2 3

解释一下为什么要 21-1：因为java进行整出运算时不会进行四舍五入，只保留整数不分。18/6 和 21/6 的结果都是3，按照每一个数字开头有 6 种排列方式，第 18和第 21 都是以 4开头。但实际上第 18 个排列以 “3” 开头，第 21 个以 “4” 开头。所以使用k-1来避免这个问题。

（2）第二步：确定第二个数字

我们已经确定了第一位数字，也就是第一位数字是 4 ，第4组。从上面的排列组合可以看出，第二位存在三种数字，每一个数字都存在两次（蓝框圈出），因此第二位数字相同的又可以看成同一组。

k= 20%(4-1)! =20%6 =2， 2/(4-2)! = 2/2 =1， 1对应未使用数字中的第二位数字 “1”，因此第二位数字为2。

将2从未使用数字中去掉，还剩：1 3

（3）第三步：确定第三个数字

第三个数字只存在两种可能了，k= 2%(4-2)! =2%2 =0，0/(4-3)!= 0/1 =0，0对应未使用数字中的第一位数字 “1”，因此第三位数字为1

将1从未使用数字中去掉，还剩：3

（4）第四步：确定第四个数字

k=0%(4-4)! = 0%1 = 0，0/(4-4)!=0/1 =0 ，0对应第一位数字，此时未使用数字中的第一位数字“3”，因此第四位数字为3.

所以第 21 个排列组合为：4213

4. 代码实现

import java.util.ArrayList;
import java.util.List;

public class PermutationSequence60 {
    public static void main(String[] args) {
        System.out.println(getPermutation(4,21));
        System.out.println(19/6);
    }
    public static String getPermutation(int n,int k){
        int pos = 0;
        List<Integer> numbers = new ArrayList<>();
        int[] factorial = new int[n+1];
        StringBuilder sb = new StringBuilder();

        int sum = 1;
        factorial[0] = 1;
        // 保存不同整数的阶乘
        for(int i=1; i<=n; i++){
            sum *= i;
            factorial[i] = sum;
        }
        // factorial[] = {1, 1, 2, 6, 24, ... n!}

        // 未使用数字列表
        for(int i=1; i<=n; i++){
            numbers.add(i);
        }

        k--;

        for(int i = 1; i <= n; i++){
            System.out.println(factorial[n-i]);
            int index = k/factorial[n-i];
            sb.append(String.valueOf(numbers.get(index)));
            numbers.remove(index);
            k =k%factorial[n-i];
        }

        return String.valueOf(sb);
    }
}