Directed Graphs

有向图

Introduction

就是边是有方向的，像单行道那样，也有很多典型的应用。

点的出度指从这个点发出的边的数目，入度是指向点的边数。当存在一条从点 v 到点 w 的路径时，称点 v 能够到达点 w ，但要注意这并不意味着点 w 可以到达点 v 。

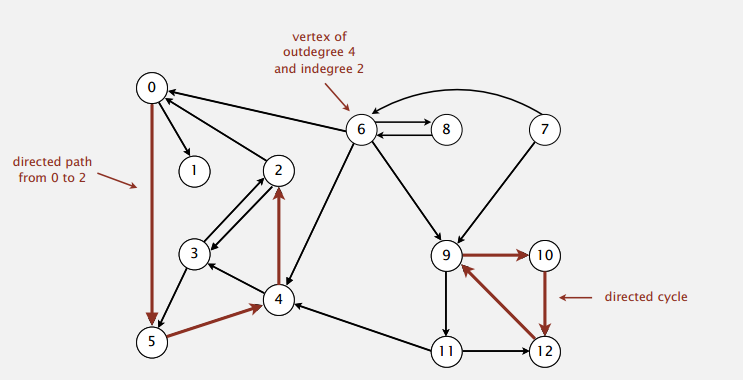
Digraph API

先给出表示有向图的 API 以及简单的测试用例，booksite-4.2 上可以找到完整的。

API

Sample Client

运行示例

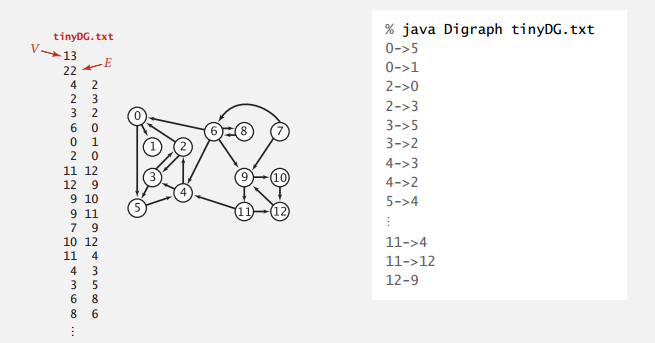
仍然使用邻接表来实现有向图，比无向图还简单其实。

Adjacency-list

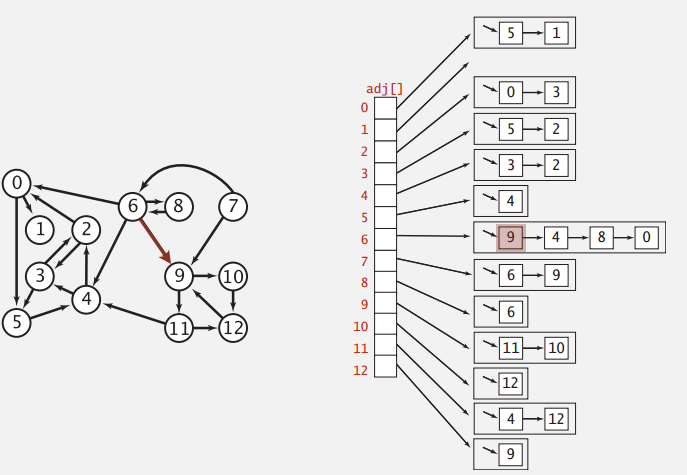
Java Implementation

public class Digraph {
    private final int V;
    private final Bag<Integer>[] adj;    // adjacency lists

    public Digraph(int V) {
        this.V = V;
        // create empty graph with V vertices
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }
    }

    // add edge v->w
    public void addEdge(int v, int w) {
        adj[v].add(w);
    }

    // iterator for vertices pointing from v
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

用邻接表来表示有向图，类似的内存使用正比于 E+V ，常数时间就能加入新边，判断点 v 到 w 是否有条边需要正比于点 v 出度的时间，遍历从点 v 发出的边也是。

Digraph Search

同样的，可以直接用 Undirected Graphs 提到的 DFS 和 BFS 这两种搜索策略。

DFS

public class DirectedDFS {
    private boolean[] marked;    // true if path from s

    // constructor marks vertices reachable from s
    public DirectedDFS(Digraph G, int s) {
        marked = new boolean[G.V()];
        dfs(G, s);
    }

    // recursive DFS does the work
    private void dfs(Digraph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    // client can ask whether any vertex is reachable from s
    public boolean visited(int v) {
        return marked[v];
    }
}

示例

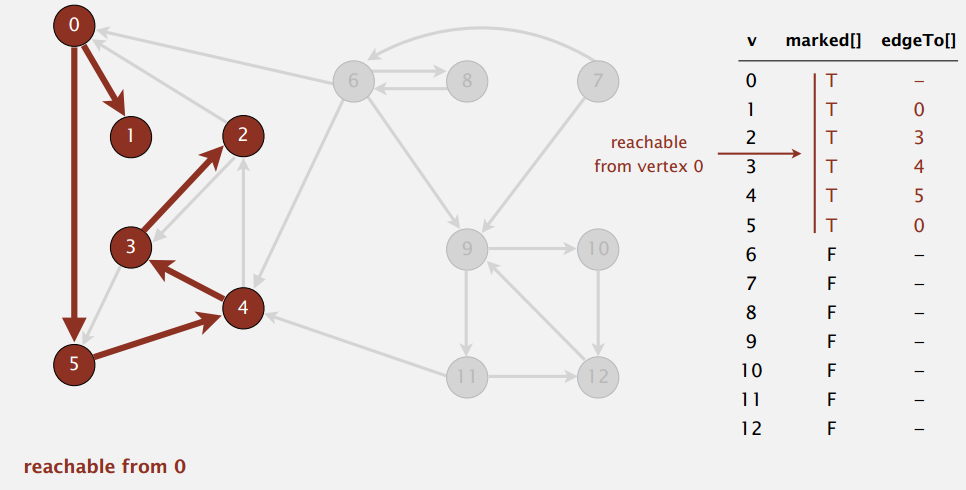
BFS

随便来张图感受一下。

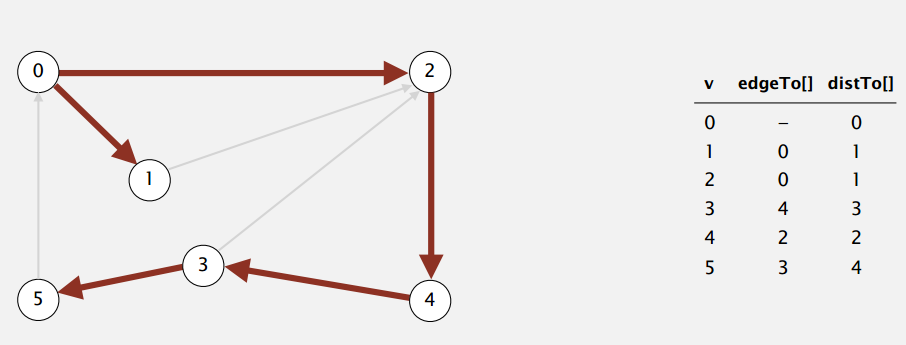
Topological Sort

拓扑排序。就是把有向图整理成箭头都朝同一个方向，像把下面的中间变成右边那种。应用也很广泛啦，比如说大学里某些课要上先修课才行，拓扑排序就可以帮我们安排课程顺序。

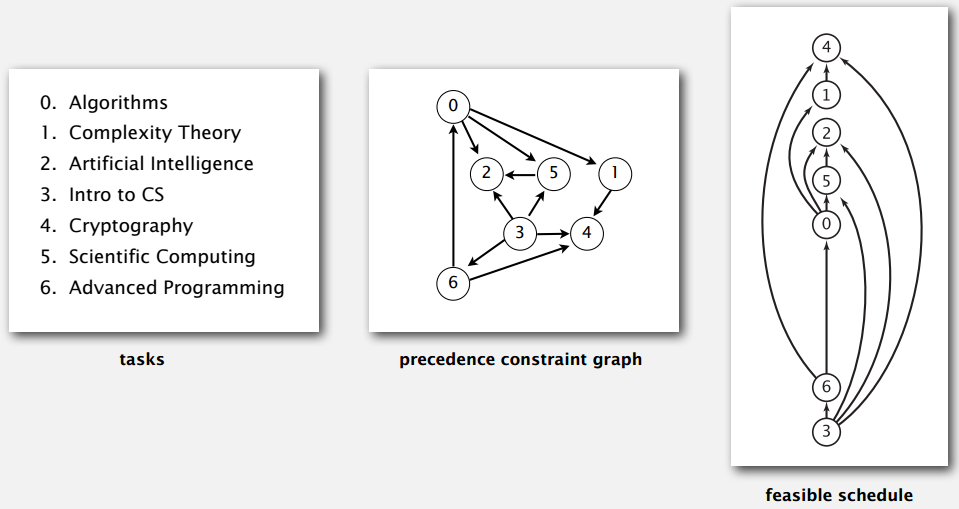
另外，拓扑排序是针对有向无环图（DAG, directed acyclic graph）来说的，设想 a 的完成依赖于 b，b 的完成又依赖于 a ，显然没有解。

Solution

DFS 稍作修改，就可以帮我们完成拓扑排序。因为 DFS 正好只会访问每个顶点一次，如果将 dfs() 参数之一的点保存在一个数据结构中，遍历这个数据结构实际上就能访问图中的所有顶点，遍历的顺序取决于这个数据结构的性质以及是在递归调用之前还是之后进行保存。在典型的应用中，人们感兴趣的是点的以下 3 种排列顺序。

• 前序（Preorder）：在递归调用之前将点加入队列。
• 后序（Postorder）：在递归调用之后将点加入队列。
• 逆后序（Reverse postorder）：在递归调用之后将点压入栈。

前序就是 dfs() 的调用顺序，后序就是点遍历完成的顺序，而逆后序就是拓扑排序。

样图

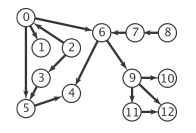
模拟

前序和后序看上图感受一下，对于逆后序就是拓扑排序可以这么想：对于任意边 v->w，在调用 dfs(v) 之时，可能的情况有三种。

• dfs(w) 已经被调用过且返回了（w 已经被标记）。
• dfs(w) 还没有被调用（w 还未被标记），因此 v->w 会直接或间接调用并返回 dfs(w)，且 dfs(w) 会在 dfs(v) 返回前返回。
• dfs(w) 已经被调用但还未返回。证明的关键在于，在 DAG 中这种情况是不可能出现的，这是由于递归调用链意味着存在从 w 到 v 的路径，再加上现在的边 v->w 则刚好补成一个环。

所以在 DAG 中只可能有前面两种情况，其中 dfs(w) 都会在 dfs(v) 之前完成，也就是说后序排序中 v 指向的点都会在其前面，那么逆后序就是把 v->w 中的 w 排在 v 后面啦。具体实现把 DFS 改一下就好，加些数据结构存点，完整示例可以参见：DepthFirstOrder.java。

Directed Cycle Detetion

上面提到过，当且仅当有向图没有有向环时，它才有拓扑排序，DFS 也能用于检测图是否含有环。因为系统维护的递归调用的栈表示的正是“当前”正在遍历的有向路径，如果我们遇到了一条边 v->w ，而 w 已经在栈里，就找到了一个环 v->w->v。

Implementation

public class DirectedCycle {
    private boolean[] marked;
    private int[] edgeTo;
    private Stack<Integer> cycle;    // 有向环中的所有顶点（如果存在）
    private boolean[] onStack;       // 递归调用的栈上的所有顶点

    public DirectedCycle (Digraph G) {
        onStack = new boolean[G.V()];
        edgeTo = new int[G.V()];
        marked = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) {
                dfs(G, v);
            }
        }
    }

    private void dfs(Digraph G, int v) {
        onStack[v] = true;    // 递归调用开始时标记为在栈中
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (this.hasCycle()) {
                return;
            }
            else if (!marked[w]) {
                edgeTo[w] = v;
                dfs(G, w);
            }
            // v->w 中 w 已经在栈中，保存环 v->w->...->v到 cycle 里
            else if (onStack[w]) {
                cycle = new Stack<Integer>();
                for (int x = v; x != w; x = edgeTo[x]) {
                    cycle.push(x);
                }
                cycle.push(w);
                cycle.push(v);
            }
            onStack[v] = false;    // 递归调用结束时标记为不在栈中
        }
    }

    public boolean hasCycle() {
        return cycle != null;
    }

    public Iterable<Integer> cycle() {
        return cycle;
    }
}

Strong Components

强连通。在有向图中，若同时存在路径 v->w 和 w->v，则称点 v 和 w 是强连通的。类似的，这显然也是一个等价关系，满足：

1. symmetric: 自反性， v 和 v 自身是强连通的。
2. reflexive: 对称性， v 和 w 强连通，则 w 和 v 强连通。
3. transitive: 传递性，如果 v 和 w 强连通，又有 w 和 x 强连通，那么 v 和 x 强连通。

强连通分量也很好理解，就是区域里面的点之间都是强连通的。

Demo

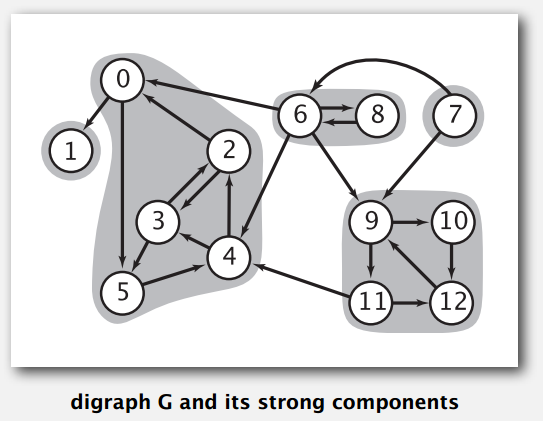
强连通分量可以帮助生物学家理解食物链中能量的流动，帮助程序员组织程序模块等。

在 Undirected Graphs 中提到的连通分量问题，可以用 DFS 预处理图，然后就可以在常数时间回应查询。同样的强连通问题也可以用 DFS 解决，用 kosaraju-sharir 算法，分成两步用两次 DFS。算法思想是计算核心 DAG （把强连通分量当成一个点）的拓扑排序，再按逆拓扑序列对点跑 DFS。我也不知道在说什么，看下面证明。

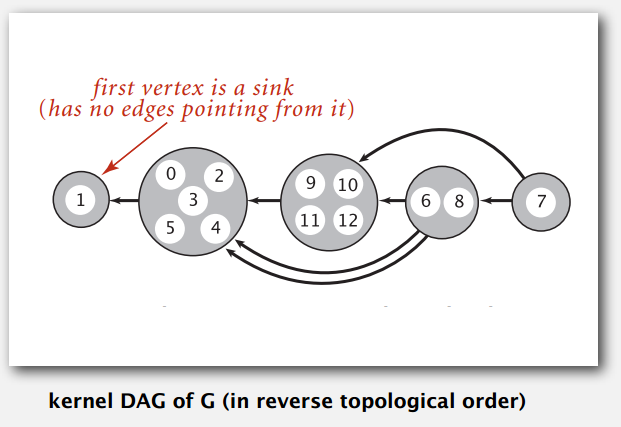
Phase 1

用 DFS 计算图 G 的反向图 \(G^{R}\) （边的方向相反）的逆后序序列。

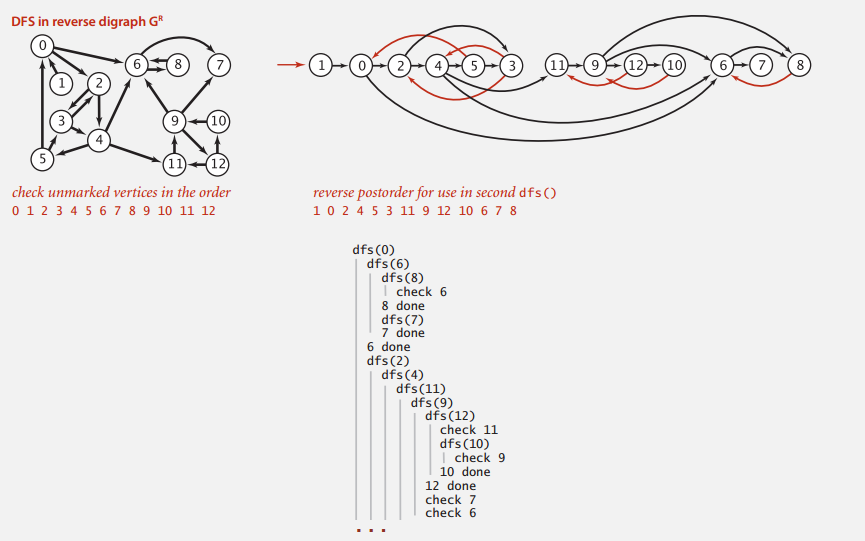
Phase 2

按第一步中的逆后序序列来对图 G 进行 DFS 。

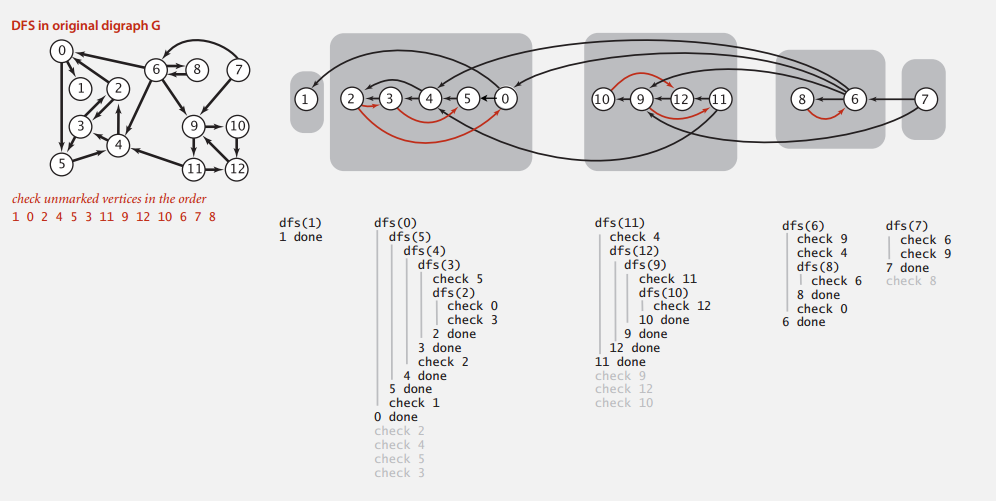
证明

分两点证明该算法的正确性。

• 第二步构造函数中调用的 dfs(G, s) 会访问每个和 s 强连通的点

  反证法。假设某个和点 s 强连通的点 v 没有在 dfs(G, s) 中被访问，那就意味着 marked[v] 为 true，即点 v 在 s 之前就已经被访问过了。又因为两点强连通，故存在着从 v 到 s 的路径，所以访问 v 的时候的 dfs(G, v) 就会调用 dfs(G, s)，而不会轮到构造函数来调用。矛盾，得证。

• 构造函数调用的 dfs(G, s) 所到达的任意点 v 都必然和 s 强连通

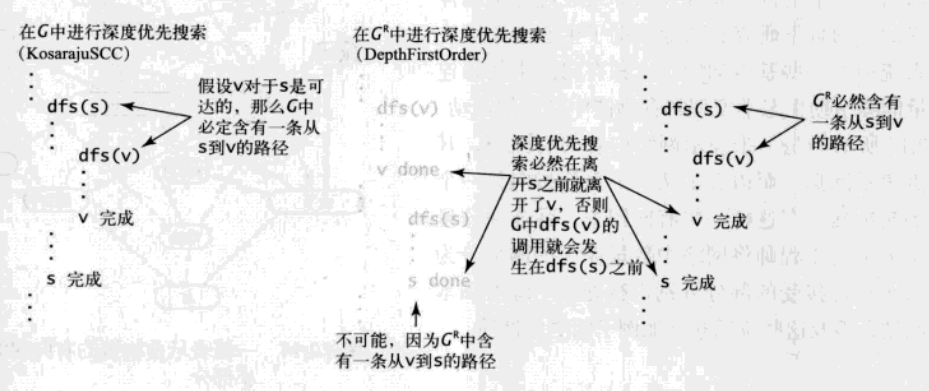
  v 能被 dfs(G, s) 访问到，说明存在路径 s->v ，那么只要再证明存在路径 v->s 就能说明两点是强连通的。即等价于在 \(G^{R}\) 中找路径 s->v，且是在已知存在路径 v->s 的前提下。因为在 \(G^{R}\) 的逆后序中 v 排在 s 后面，所以 dfs(G, v) 结束得比 dfs(G, s) 早，那就只有两种情况：

  1. 调用 dfs(G, v) 结束在调用 dfs(G, s) 开始之前。
  2. 调用 dfs(G, v) 开始在 dfs(G, s) 调用开始之后且结束在 dfs(G, s) 结束之前。

  又因为已知存在路径 v->s ，所以第一种情况是不可能的，而第二种则意味着存在路径 s->v，证毕，再来张没什么大用的图。

实现

实现只要对 Undirected Graphs 中的 “Implementation With DFS” 代码稍作修改就好其实。

public class KosarajuSharirSCC {
    private boolean[] marked;
    private int[] id;
    private int count;

    public KosarajuSharirSCC(Digraph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];
        DepthFirstOrder dfs = new DepthFirstOrder(G.reverse());
        // 按逆后序进行 DFS
        for (int v : dfs.reversePost()) {
            if (!marked[v]) {
                dfs(G, v);
                count++;
            }
        }
    }

    private void dfs(Digraph G, int v) {
        marked[v] = true;
        id[v] = count;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    public boolean stronglyConnected(int v, int w) {
        return id[v] == id[w];
    }
}