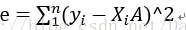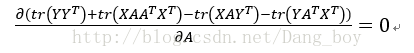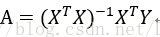岭回归&Lasso回归
转自:https://blog.csdn.net/dang_boy/article/details/78504258
https://www.cnblogs.com/Belter/p/8536939.html
https://www.cnblogs.com/Belter/p/8536939.html (这个也写的很好,只不过还没看)
1.最小二乘法则
假设我们有n个样本数据,每个数据有p个特征值,然后p个特征值是线性关系。
即对应的线性模型
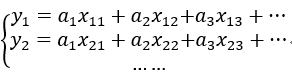
写成矩阵的形式即是Y=XA,误差B矩阵:即B=Y-XA。【Y和A是列向量,X是矩阵】
误差的平方的计算公式
Xi为行向量,A为列向量。
最小二乘法的目标就是取得最小的e对应的A,由于方差的计算是一个二次函数,即抛物线,对应存在一个最小值,即导数为0对应的A。所以对e求A的偏导数,再使其等于0,求解方程即可以获得A。
误差的平方e写成矩阵形式即为
对矩阵E取迹(迹就是矩阵对角线上所有元素的累加)且对迹求导后结果为一个矩阵。
即为
展开为
求导化简结果为
注:这个计算的过程是涉及到向量的求导运算,看了好长时间实在是看不懂。也不知道这个结果是怎么计算出来的,暂且记住吧。。
参考:https://blog.csdn.net/lipengcn/article/details/52815429
当A的维数比Y的维数多,即样本数量n少于特征值p的时候存在多个解,可能导致结果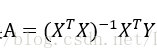
X矩阵不存在广义逆(即奇异性)的情况:
1)X本身存在线性相关关系(即多重共线性),即非满秩矩阵。
当采样值误差造成本身线性相关的样本矩阵仍然可以求出逆阵时,此时的逆阵非常不稳定,所求的解也没有什么意义。
2)当变量比样本多,即p>n时.
这时,回归系数会变得很大,无法求解。在统计学上,可证明A的最小二乘解为无偏估计,即多次得到的采样值X而计算出来的多个系数估计值向量 的平均值将无限接近于真实值向量β。
2.岭回归
那么解决不存在矩阵广义逆:
在误差矩阵加上一个对A的L2范数控制系数矩阵,
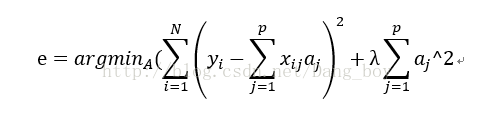
而LASSO回归是加上的L1范数作为正则项。
反映到矩阵上,就是在原先的A的最小二乘估计中加一个小扰动λI,
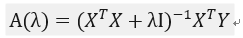
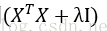
具体推导过程就不贴了,贴了也看不懂。
3.LASSO回归
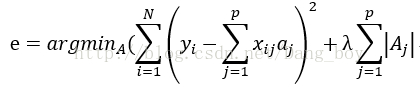
只是在于正则项的不同。
4.对于偏差与方差的理解
看到这个图觉得很不错:
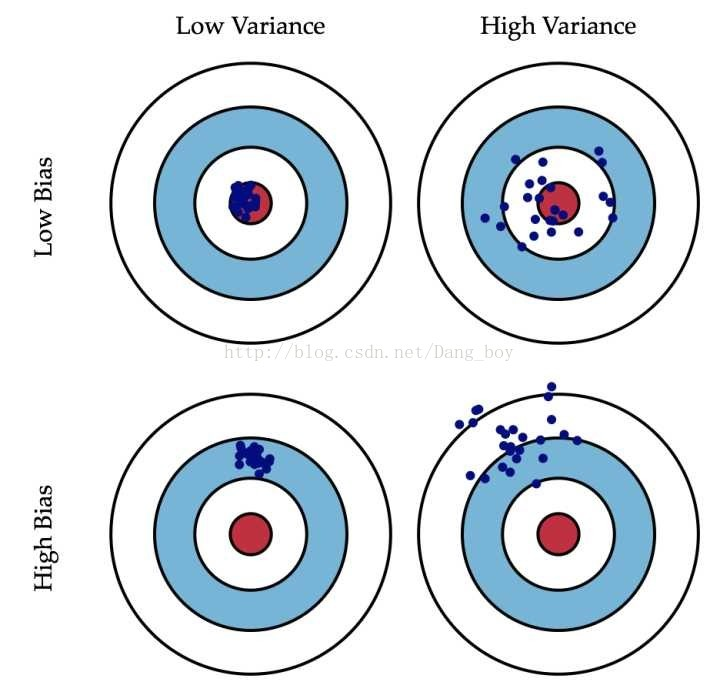
偏差:预测出来的数据与真实值的差距
方差:预测出来的数据的分散程度
岭回归&Lasso回归的更多相关文章
- 笔记︱范数正则化L0、L1、L2-岭回归&Lasso回归(稀疏与特征工程)
机器学习中的范数规则化之(一)L0.L1与L2范数 博客的学习笔记,对一些要点进行摘录.规则化也有其他名称,比如统计学术中比较多的叫做增加惩罚项:还有现在比较多的正则化. -------------- ...
- 【机器学习】正则化的线性回归 —— 岭回归与Lasso回归
注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基本原理有一个透彻.直观的理解.直到最近再次接触到这个概念 ...
- 线性回归——lasso回归和岭回归(ridge regression)
目录 线性回归--最小二乘 Lasso回归和岭回归 为什么 lasso 更容易使部分权重变为 0 而 ridge 不行? References 线性回归很简单,用线性函数拟合数据,用 mean squ ...
- 机器学习之五 正则化的线性回归-岭回归与Lasso回归
机器学习之五 正则化的线性回归-岭回归与Lasso回归 注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基 ...
- 机器学习:模型泛化(LASSO 回归)
一.基础理解 LASSO 回归(Least Absolute Shrinkage and Selection Operator Regression)是模型正则化的一定方式: 功能:与岭回归一样,解决 ...
- 多元线性回归模型的特征压缩:岭回归和Lasso回归
多元线性回归模型中,如果所有特征一起上,容易造成过拟合使测试数据误差方差过大:因此减少不必要的特征,简化模型是减小方差的一个重要步骤.除了直接对特征筛选,来也可以进行特征压缩,减少某些不重要的特征系数 ...
- 机器学习--Lasso回归和岭回归
之前我们介绍了多元线性回归的原理, 又通过一个案例对多元线性回归模型进一步了解, 其中谈到自变量之间存在高度相关, 容易产生多重共线性问题, 对于多重共线性问题的解决方法有: 删除自变量, 改变数据形 ...
- 通俗易懂--岭回归(L2)、lasso回归(L1)、ElasticNet讲解(算法+案例)
1.L2正则化(岭回归) 1.1问题 想要理解什么是正则化,首先我们先来了解上图的方程式.当训练的特征和数据很少时,往往会造成欠拟合的情况,对应的是左边的坐标:而我们想要达到的目的往往是中间的坐标,适 ...
- 岭回归和Lasso回归以及norm1和norm2
norm代表的是距离,两个向量的距离:下图代表的就是p-norm,其实是对向量里面元素的一种运算: 最简单的距离计算(规范)是欧式距离(Euclidean distance),两点间距离是如下来算的, ...
随机推荐
- ubuntu下vim配置(刷题和比赛两套)
1. 平时刷题练习使用 "mswin.vim 插件提供windows下的编辑快捷键功能 source $VIMRUNTIME/mswin.vim behave mswin set nu se ...
- POJ 1273 Drainage Ditches (网络最大流)
http://poj.org/problem? id=1273 Drainage Ditches Time Limit: 1000MS Memory Limit: 10000K Total Sub ...
- HTML&CSS精选笔记_布局与兼容性
布局与兼容性 CSS布局 版心和布局流程 为什么要应用布局? 阅读报纸时容易发现,虽然报纸中的内容很多,但是经过合理地排版,版面依然清晰.易读.同样,在制作网页时,要想使页面结构清晰.有条理,也需要对 ...
- 【RF库Collections测试】Get From Dictionary
Name:Get From DictionarySource:Collections <test library>Arguments:[ dictionary | key ]Returns ...
- 对double数据类型的数据保留两位小数,并且进行四舍五入
1.代码如下: /** * 对double数据类型的数据 保留两位小数,并且进行四舍五入 * @author Administrator */ public class Main { // 工具类 p ...
- Redis(四)-- 集群
一.Redis适合做企业级分布式缓存集群的条件 1.Redis内置哈希槽,有16384个哈希槽(0~16383),根据CRC16算法来确定这个集群中属于哪一个服务器来处理这个请求. 2.Redis提供 ...
- len()
len() 用于统计序列的长度,字符串 .元组 .列表都属于序列 In [1]: str = "hello world" In [2]: len(str) Out[2]: 11
- webstrom如何配置babel来转换es6
网上有很多关于如何设置babel的.我学习着设置,但总差那么几步,没能满足我的需求. 我使用的是webStorm2017.1版本. babel安装准备 使用webStorm自带的filewatcher ...
- BSTR与char*、cstring、CComBSTR的转换
// BSTR_Convert.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <comutil.h> // ...
- C++中的抽象基类示例
抽象基类(abstract base class,ABC)例子:圆与椭圆.建立一个基类BaseEllipse,建立它的恋歌继承了Ellipse和Circle.ellipse.h #ifndef ELL ...