红黑树(Red-Black Tree)，B树，B-树，B+树，B*树

（一）红黑树（Red-Black Tree）

http://www.cnblogs.com/skywang12345/p/3245399.html#a1

它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

红黑树的特性:

（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：
特性(3)中的叶子节点，是只为空(NIL或null)的节点。
特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

红黑树的示意图如下：

　　　　　　　　　　　　　　　　　　

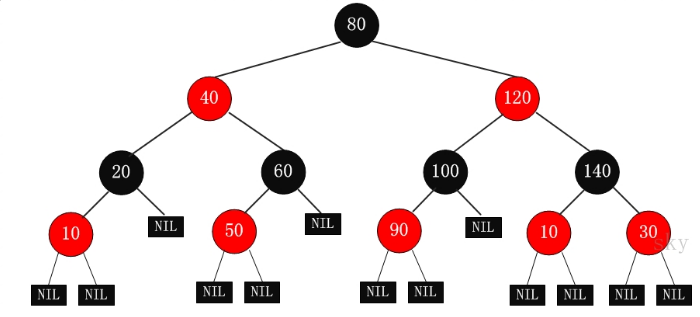
红黑树的应用：

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。
例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

（二）B树

　　即二叉搜索树

　　1，所有的非叶子节点最多有两个孩子节点（LeftChild and RightChild）

　　2，所有的节点存储一个关键字

　　3，非叶子节点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

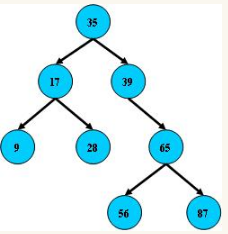
（三）B- 树

　　是一颗多路搜索树（不是二叉树）

　　1，定义任意非叶子节点最多有M个孩子，M>2

　　2，根节点的儿子数范围为 【2，M】，，除非根结点为叶子节点；

　　3,除根结点以外的非叶子结点的儿子数为[M/2, M]；

　　4, 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

　　5,非叶子结点的关键字个数=指向儿子的指针个数-1；

　　6,非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

　   7,非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，

　　其它P[i]指向关键字属于 ( K[i-1], K[i] ) 的子树；

　　8,所有叶子结点位于同一层；

　　例如：（M=3）

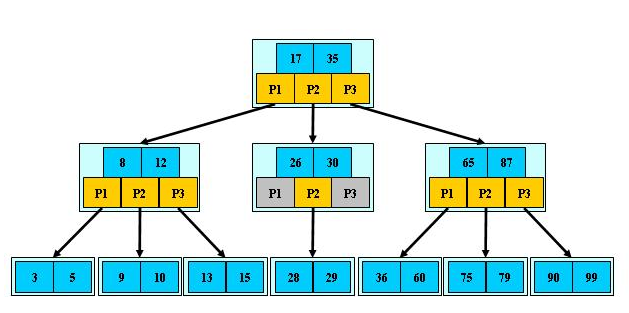
　　B-tree有以下特性：

　　　　1、关键字集合分布在整棵树中；

　　　　2、任何一个关键字出现且只出现在一个结点中；

　　　　3、搜索有可能在非叶子结点结束；

　　　　4、其搜索性能等价于在关键字全集内做一次二分查找；

　　　　5、自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少

利用率，其最底搜索性能为：O[Log₂N]，  其中，M为设定的非叶子结点最多子树个数，N为关键字总数；所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

　　由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

（四）B+树

　　 B+树是B-树的变体，也是一种多路搜索树：

　　 1.其定义基本与B-树同，除了：

　　 2.非叶子结点的子树指针与关键字个数相同；

　　 3.非叶子结点的子树指针P[i]，指向关键字值属于 [ K[i], K[i+1] ) 的子树

　　　　（B-树是开区间）；

　　5.为所有叶子结点增加一个链指针；

　　 6.所有关键字都在叶子结点出现；

　　   如：（M=3）

　　　　　　　　　　　　　　

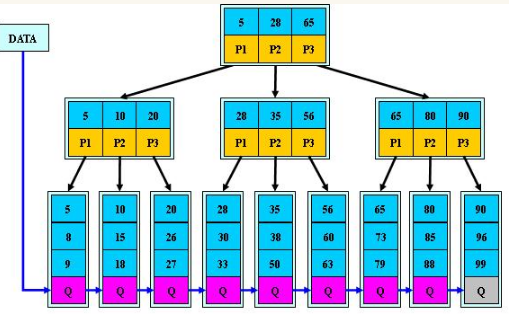
　　B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

　　  B+的特性：

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2.不可能在非叶子结点命中；

3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4.更适合文件索引系统；

 （五）B*树

　　是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；

　　　　　　　　　　　　 

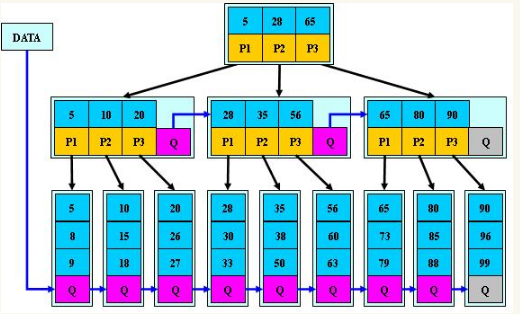
　B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）；

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；,

小结：

1， B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

2，B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点； 所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

3，B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

4，B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；