Codeforces 463D Gargari and Permutations：隐式图dp【多串LCS】

题目链接：http://codeforces.com/problemset/problem/463/D

题意：

　　给你k个1到n的排列，问你它们的LCS（最长公共子序列）是多长。

题解：

　　因为都是1到n的排列，即每个串中，1到n每个数字恰好出现一次。

　　将相同的数字之间相连，可以得到下面的样子(n = 4, k = 3)：

　　

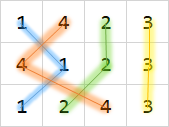
　　显然，要求的LCS就等于图中互不相交的最多连线个数。

　　将每一个数字看做一个节点。

　　若i到j有一条有向边，则代表：

　　　　数字j的连线在i的连线的后面，且互不相交。

　　即：

　　　　若i->j，则要满足所有的pos[k][i] <= pos[k][j]。

　　　　其中pos[k][i]表示第k个串中，数字i出现的位置。

　　O(N^2*K)建图，最终得到的一定是一个有向无环图。

　　LCS就等于这个图上的最长路径长度。

　　所以dfs跑一边dp就行了。

AC Code:

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #include <vector>
 #define MAX_N 1005
 #define MAX_K 10

 using namespace std;

 int n,k;
 int dp[MAX_N];
 int a[MAX_K][MAX_N];
 int pos[MAX_K][MAX_N];
 vector<int> edge[MAX_N];

 void read()
 {
     cin>>n>>k;
     for(int i=;i<=k;i++)
     {
         for(int j=;j<=n;j++)
         {
             cin>>a[i][j];
             pos[i][a[i][j]]=j;
         }
     }
 }

 bool is_valid(int x,int y)
 {
     for(int i=;i<=k;i++)
     {
         if(pos[i][x]>=pos[i][y]) return false;
     }
     return true;
 }

 void build()
 {
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=n;j++)
         {
             if(is_valid(i,j)) edge[i].push_back(j);
         }
     }
 }

 void dfs(int now)
 {
     dp[now]=;
     for(int i=;i<edge[now].size();i++)
     {
         int temp=edge[now][i];
         if(dp[temp]==-) dfs(temp);
         dp[now]=max(dp[now],dp[temp]+);
     }
 }

 void work()
 {
     build();
     memset(dp,-,sizeof(dp));
     int ans=;
     for(int i=;i<=n;i++)
     {
         if(dp[i]==-) dfs(i);
         ans=max(ans,dp[i]);
     }
     cout<<ans<<endl;
 }

 int main()
 {
     read();
     work();
 }