hdu 4587(枚举+割顶）

TWO NODES

Time Limit: 24000/12000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 2354    Accepted Submission(s): 780

Problem Description

Suppose that G is an undirected graph, and the value of stab is defined as follows:

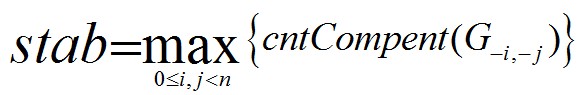
Among the expression,G_{-i, -j} is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.

Input

The
input will contain the description of several graphs. For each graph,
the description consist of an integer N for the number of nodes, an
integer M for the number of edges, and M pairs of integers for edges
(3<=N,M<=5000).
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.

Output

For each graph in the input, you should output the value of stab.

Sample Input

4 5

0 1

1 2

2 3

3 0

0 2

Sample Output

2

Source

2013 ACM-ICPC南京赛区全国邀请赛——题目重现

 题意：在一个无向图中，删除两个点，使的连通分量最大 输出最大的联通分量

枚举一个点 然后在剩下的n个点中选取一个点做顶点 然后利用割顶的性质判断这n-1个点的可以拆成多少个联通分量

其实就是在判断割顶的地方iscut[u]++;

但我们需要注意的是当选取的点是根节点时：incut[u]=0,因为他是没有父亲的，意思就是上面没有联通分量了

所以不是根节点的初始值就是iscut[u]=1，因为他的父亲那块是一个联通分量

由于删点会导致这个图不联通，所以需要DFS，看有几个联通块sum

最后的答案就是 max(sum+iscut[i]-1)

这个减1是因为将一个联通块拆成iscut[i]个 那么本身的联通块就没有了

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<string.h>
 #include<set>
 #include<vector>
 #include<queue>
 #include<stack>
 #include<map>
 #include<cmath>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const double PI=acos(-1.0);
 const double eps=0.0000000001;
 const int INF=1e9;
 const int N=+;
 int head[N];
 int t,tot;
 struct node{
     int to,next;
 }edge[N<<];
 int low[N];
 int dfn[N];
 int iscut[N];
 void init(){
     memset(low,,sizeof(low));
     memset(dfn,,sizeof(dfn));
     t=;
 }
 void add(int u,int v){
     edge[tot].to=v;
     edge[tot].next=head[u];
     head[u]=tot++;
 }
 int DFS(int u,int fa,int flag){
     low[u]=dfn[u]=++t;
     int child=;
     for(int i=head[u];i!=-;i=edge[i].next){
         int v=edge[i].to;
         if(v==flag)continue;
         if(dfn[v]==){
             child++;
             int lowv=DFS(v,u,flag);
             low[u]=min(low[u],lowv);
             if(lowv>=dfn[u]){
                 iscut[u]++;
             }
         }
         else if(dfn[v]<dfn[u]&&v!=fa){
             low[u]=min(low[u],dfn[v]);
         }
     }
     if(fa<&&child==)low[u]=;
     return low[u];
 }
 int main(){
     int n,m;
     while(scanf("%d%d",&n,&m)!=EOF){
         memset(head,-,sizeof(head));
         tot=;
         for(int i=;i<=m;i++){
             int u,v;
             scanf("%d%d",&u,&v);
             add(u,v);
             add(v,u);
         }
         int ans=;
         for(int i=;i<n;i++){
             int sum=;
             init();
             for(int j=;j<n;j++){
                 iscut[j]=;
             }
             iscut[i]=;
             for(int j=;j<n;j++){
                 if(i==j)continue;
                 if(dfn[j])continue;
                 iscut[j]=;
                 sum++;
                 DFS(j,-,i);

             }
             for(int j=;j<n;j++){
                 ans=max(ans,iscut[j]+sum-);
             }
         }
         cout<<ans<<endl;
     }
 }