算法复习——半平面交（bzoj2618凸多边形）

讲解：

这里套用wuvin神犇的ppt，附上友情链接：http://blog.leanote.com/wuvin

半平面交：

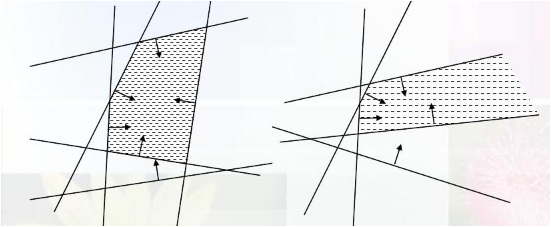
算法流程：

注意事项：

例题：

Description

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：

 

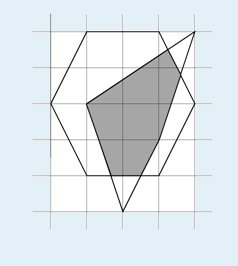
则相交部分的面积为5.233。

Input

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数m_i，表示多边形的边数，以下m_i行每行两个整数，逆时针给出各个顶点的坐标。

Output

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

Sample Input

2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0

Sample Output

5.233

HINT

100%的数据满足：2<=n<=10，3<=m_i<=50，每维坐标为[-1000,1000]内的整数

题解：

　　半平面交裸题

心得：

　　主要是代码很烦吧···一定要理清点与点之间的关系，多画图帮助理解；

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
struct point
{
  double x;
  double y;
}p[N],a[N];
struct line
{
  point a;
  point b;
  double slope;
}l[N],q[N];
inline double operator * (point a,point b)
{
  return a.x*b.y-a.y*b.x;
}
inline point operator - (point a,point b)
{
  point t;
  t.x=a.x-b.x;
  t.y=a.y-b.y;
  return t;
}
inline point inter(line a,line b)
{
  double k1=(b.b-a.a)*(a.b-a.a);
  double k2=(a.b-a.a)*(b.a-a.a);
  double t=k1/(k1+k2);
  point k;
  k.x=b.b.x+(b.a.x-b.b.x)*t;
  k.y=b.b.y+(b.a.y-b.b.y)*t;
  return k;
}
bool jud(line a,line b,line c)
{
  point t=inter(a,b);
  return (t-c.a)*(c.b-c.a)>;
}
int n,k,cnt,tot;
double ans;
bool comp(line a,line b)
{
  if(a.slope!=b.slope)  return a.slope<b.slope;
  else return (b.b-a.a)*(a.b-a.a)<;
}
void build()
{
  sort(l+,l+cnt+,comp);
  /*for(int i=1;i<=cnt;i++)
    cout<<l[i].a.x<<' '<<l[i].a.y<<' '<<l[i].b.x<<' '<<l[i].b.y<<endl;*/
  for(int i=;i<=cnt;i++)
  {
    if(l[i].slope!=l[i-].slope)tot++;
    l[tot]=l[i];
  }
  int left=,right=;
  q[++right]=l[];
  q[++right]=l[];
  cnt=tot,tot=;
  for(int i=;i<=cnt;i++)
  {
    while(left<right&&jud(q[right-],q[right],l[i]))  right--;
    while(left<right&&jud(q[left+],q[left],l[i]))  left++;
    q[++right]=l[i];
  }
  while(left<right&&jud(q[right-],q[right],q[left]))  right--;
  while(left<right&&jud(q[left+],q[left],q[right]))  left++;
  q[right+]=q[left];
  for(int i=left;i<=right;i++)
    a[++tot]=inter(q[i],q[i+]);

}
void getans()
{
  if(tot<)  return;
  a[tot+]=a[];
  for(int i=;i<=tot;i++)
    ans+=a[i]*a[i+];
  ans=fabs(ans)/;
}
int main()
{
  //freopen("a.in","r",stdin);
  scanf("%d",&n);
  for(int i=;i<=n;i++)
  {
    scanf("%d",&k);
    for(int j=;j<=k;j++)
      scanf("%lf%lf",&p[j].x,&p[j].y);
    p[k+]=p[];
    for(int j=;j<=k;j++)
    {
      l[++cnt].a=p[j];
      l[cnt].b=p[j+];
    }
  }
  /*for(int i=1;i<=cnt;i++)
    cout<<l[i].a.x<<' '<<l[i].a.y<<' '<<l[i].b.x<<' '<<l[i].b.y<<endl;*/
  for(int i=;i<=cnt;i++)
    l[i].slope=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
  build();
  getans();
  printf("%.3lf\n",ans);
  return ;
}