POJ 3463 Sightseeing （次短路经数）

　　　　　　　　　　　　　　　　　　　　Sightseeing

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions:10005		Accepted: 3523

Description

Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.

Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.

There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.

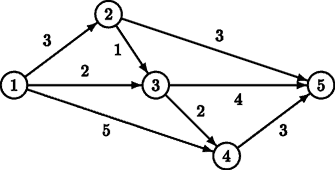
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.

Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.

Input

The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

• One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.

• M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.

  The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.

• One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.

  There will be at least one route from S to F.

Output

For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10⁹ = 1,000,000,000.

Sample Input

2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1

Sample Output

3
2

Hint

The first test case above corresponds to the picture in the problem description.

思路

一开始我想了一下，用A*好像可以做，但是超了内存，看了一下discuss，原因应该是不断入队造成的，这让我感到十分无奈，毕竟刚刚才用a*过了一题。

具体的东西我写在注释里了，注意次短路的入队操作！

#include<iostream>
#include<vector>
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const ll inf = 210000000000000;
int n,m,s,t;
vector<int>u[1024];
vector<ll>w[1024];
ll dis[1024][2];
//虽然按照我的推理，这个题不会爆int ，可是不用int，就是会wa;
bool book[1024][2];
ll ans[1024][2];
struct node
{
    int num;
    ll dis;
    int flag;
    bool operator<(const node x)const
    {
        return x.dis<dis;
    }
};

ll Dijkstra()
{
    priority_queue<node>q;
    node exa;
    dis[s][0]=0;ans[s][0]=1;
    q.push(node{s,0,0});
    while(!q.empty()){
        exa=q.top();q.pop();
        int st = exa.num;//当前起点
        ll diss=exa.dis;//diss表示，当前节点的最短（或次短）
        int f=exa.flag;//表示这是最短还是次短
        if(book[st][f]){continue;}
        book[st][f]=true;
        int siz=u[st].size();
        for(int i=0;i<siz;i++){
            int y=u[st][i];
            ll ww=w[st][i];
            /*y是下一个节点，ww是路径*/
            if(dis[y][0]>diss+ww){//最短的距离可以更新
                q.push(node{y,dis[y][0],1});
                dis[y][1]=dis[y][0];//下一节点的次短路，就是更新前的最短路
                ans[y][1]=ans[y][0];//下一节点的次短路条数，就是更新前的最短路条数
                dis[y][0]=diss+ww;//更新最短路
                ans[y][0]=ans[st][0];//下一最短路的条数，就是当前节点最短/次短的条数
                                        //这个位置不可能是次短路更新
                q.push(node{y,diss+ww,0});
            }
            else if(dis[y][0]==diss+ww){//下一节点的最短距离，就是当前距离
                ans[y][0]+=ans[st][0];
            }
            else if(dis[y][1]>diss+ww){//次短路可更新
                dis[y][1]=diss+ww;//更新次短路
                ans[y][1]=ans[st][f];//下一节点的次短路条数，就是更新来源的路径数
                q.push(node{y,diss+ww,1});
            }
            else if(dis[y][1]==diss+ww){
                ans[y][1]+=ans[st][f];//下一节点的路径数，加上当前节点的路径数
            }
        }
    }
    if(dis[t][1]==dis[t][0]+1){
        return ans[t][0]+ans[t][1];
    }
    return ans[t][0];
}

void init()
{
    for(int i=0;i<=n+1;i++){
        for(int j=0;j<=1;j++){
            dis[i][j]=inf;
        }
    }
    memset(book,0,sizeof(book));
    memset(ans,0,sizeof(ans));
    for(int i=1;i<=n;i++){
        u[i].clear();
        w[i].clear();
    }
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        init();
        int x,y;ll z;
        for(int i=1;i<=m;i++){
            scanf("%d%d%lld",&x,&y,&z);
            u[x].push_back(y);
            w[x].push_back(z);
        }
        scanf("%d%d",&s,&t);
        printf("%lld\n",Dijkstra());
    }
}

　　妈呀，wa死我了，a个题真不容易