NOIP2018保卫王国

题目大意：给一颗有点权的树，每次规定两个点选还是不选，求这棵树的最小权点覆盖。

题解

ZZ码农题。

要用动态dp做，这题就是板子，然鹅并不会，留坑代填。

因为没有修改，所以可以静态倍增。

我们先做一遍正常的树形dp，求出g[i][0/1]，0/1表示当前节点选或不选。

然后我们再倒腾出一个数组l[i][0/1]表示从当前点作为根，再扣掉当前子树的答案。

然后倍增处理dp[i][j][0/1][0/1]表示从i向上2ⁱ长度的链，起点和终点的选择情况，表示以下区域的答案。

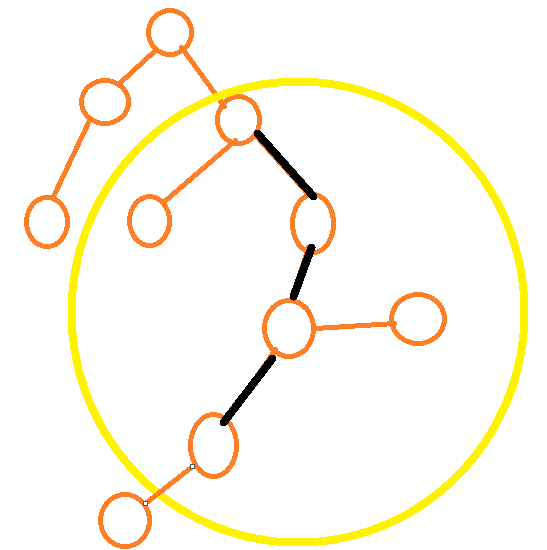
比如这条黑色的链，它表示的是黄圈里的所有点的答案。

然后对于一个询问，我们可以跳LCA，边跳变统计答案，这样我们就可以统计出以LCA为根的子树的答案，在加上之前处理过的l数组的答案，就可以吧答案算全了。

NOIP考这种****题有意思吗？

代码

#include<iostream>
#include<cstdio>
#define N 100009
using namespace std;
typedef long long ll;
int tot,head[N],deep[N],p[N][],n,m;
char typef[];
ll dp[N][][][],w[N],f[][],g[][],pr[N][],lian[N][],pr2[N][];
inline int rd(){
    int x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
struct node{int n,to;}e[N<<];
inline void add(int u,int v){e[++tot].n=head[u];e[tot].to=v;head[u]=tot;}
inline void hb(int x,int y,int l){
    dp[x][l][][]=min(dp[x][l-][][]+dp[y][l-][][],dp[x][l-][][]+dp[y][l-][][]);
    dp[x][l][][]=min(dp[x][l-][][]+dp[y][l-][][],dp[x][l-][][]+dp[y][l-][][]);
    dp[x][l][][]=min(dp[x][l-][][]+dp[y][l-][][],dp[x][l-][][]+dp[y][l-][][]);
    dp[x][l][][]=min(dp[x][l-][][]+dp[y][l-][][],dp[x][l-][][]+dp[y][l-][][]);
}
void dfs(int u,int fa){
    for(int i=;(<<i)<=deep[u];++i){
        p[u][i]=p[p[u][i-]][i-];
        hb(u,p[u][i-],i);
    }
    for(int i=head[u];i;i=e[i].n)if(e[i].to!=fa){
        int v=e[i].to;deep[v]=deep[u]+;p[v][]=u;
        dp[v][][][]=pr[u][]-min(pr[v][],pr[v][]);
        dp[v][][][]=pr[u][]-pr[v][];
        dp[v][][][]=pr[u][]-min(pr[v][],pr[v][]);
        dfs(v,u);
    }
}
void predfs(int u,int fa){
    pr[u][]=;pr[u][]=w[u];
    for(int i=head[u];i;i=e[i].n)if(e[i].to!=fa){
        int v=e[i].to;predfs(v,u);
        pr[u][]+=pr[v][];pr[u][]+=min(pr[v][],pr[v][]);
    }
}
void dfs2(int u,int fa){
    for(int i=head[u];i;i=e[i].n)if(e[i].to!=fa){
        int v=e[i].to;
    //    pr2[v][0]=pr2[u][1];pr2[v][1]=min(pr2[u][0],pr2[u][1]);
    //    lian[v][0]=pr2[v][0]-pr[v][0];lian[v][1]=pr2[v][1]-pr[v][1];
       lian[v][]=lian[u][]+pr[u][]-min(pr[v][],pr[v][]);
       lian[v][]=min(lian[v][],lian[u][]+pr[u][]-pr[v][]);
        dfs2(v,u);
    }
}
inline ll getlca(int a,int b,int x,int y){
    if(deep[a]<deep[b])swap(a,b),swap(x,y);
//    cout<<a<<" "<<b<<" "<<x<<" "<<y<<endl;
    ll ans=pr[a][x]; //cout<<ans<<endl;
    f[][x]=;int now=,pre=;
    for(int i=;i>=;--i)if(deep[a]-(<<i)>=deep[b]){
        f[now][]=min(f[pre][]+dp[a][i][][],f[pre][]+dp[a][i][][]);
        f[now][]=min(f[pre][]+dp[a][i][][],f[pre][]+dp[a][i][][]);
        swap(now,pre);a=p[a][i];
    }
    if(a==b)return ans+f[pre][y]+lian[a][y];
    g[pre][y]=;ans+=pr[b][y];//cout<<ans<<endl;
    for(int i=;i>=;--i)if(p[a][i]!=p[b][i]){
        f[now][]=min(f[pre][]+dp[a][i][][],f[pre][]+dp[a][i][][]);
        f[now][]=min(f[pre][]+dp[a][i][][],f[pre][]+dp[a][i][][]);
        g[now][]=min(g[pre][]+dp[b][i][][],g[pre][]+dp[b][i][][]);
        g[now][]=min(g[pre][]+dp[b][i][][],g[pre][]+dp[b][i][][]);
        swap(now,pre);a=p[a][i];b=p[b][i];
    }
    swap(now,pre);
    ll ans1=f[now][]+g[now][]+pr[p[a][]][]-pr[a][]-pr[b][];
    ll ans2=min(f[now][],f[now][])+min(g[now][],g[now][])+pr[p[a][]][]-min(pr[a][],pr[a][])-min(pr[b][],pr[b][]);
    return ans+min(ans1+lian[p[a][]][],ans2+lian[p[a][]][]);
}
int main(){
    n=rd();m=rd();scanf("%s",typef);int u,v;
    for(int i=;i<=n;++i)w[i]=rd();
    for(int i=;i<=n;++i)
      for(int j=;j<=;++j)
       for(int k=;k<=;++k)for(int l=;l<=;++l)dp[i][j][k][l]=1e12;
    for(int i=;i<n;++i){u=rd();v=rd();add(u,v);add(v,u);}
    predfs(,);
    pr2[][]=pr[][];pr2[][]=pr[][];dfs2(,);
    dfs(,);int a,x,b,y;
/*    for(int i=1;i<=n;++i){
        cout<<i<<" ";
      for(int j=0;j<=1;++j)cout<<lian[i][j]<<" ";cout<<endl;
    }*/
  /*  for(int i=1;i<=n;++i){
        cout<<i<<endl;
        for(int j=0;(1<<j)<=deep[i];++j)cout<<dp[i][j][0][0]<<" "<<dp[i][j][0][1]<<" "<<dp[i][j][1][0]<<" "<<dp[i][j][1][1]<<endl;
    }*/
    while(m--){
        a=rd();x=rd();b=rd();y=rd();
        for(int i=;i<=;++i)for(int j=;j<=;++j)f[i][j]=g[i][j]=1e12;
        ll ans=getlca(a,b,x,y);
        if(ans>1e10)puts("-1");else printf("%lld\n",ans);
    }
    return ;
}