MindFusion 中节点关键路径的遍历

　　工作中总能遇到 一些 奇葩的需求，提出这些奇葩需求的人，多半也是奇葩的人，要么不懂相关的计算机软件知识，要么就是瞎扯蛋，异想天开，然而这些奇葩的需求，我也总能碰到。言规正传，在一次项目中，使用了 MindFusion 这个组件，在 Winform  窗体中画一些工序（生产中的工艺流程）节点，然后在工序节点间建立有向箭头连线，以此来表示工序的顺序，并行关系。因为有很多工序，每个工序都有一个持续时间，来表示该工序要多少时间才能完成，以天为单位，为了明确整个工序的工期，我们组的领导，想到用项目管理中的关键路径 （从工期开始到结束累计持续时间最长的一条或几条路径）来表示，这个倒是可以的，但是，项目中的每个工序的持续时间有问题，要么是0，要么是-1，要么是大于0的数字，这个就不能用关键路径的算法 来求了，而且工序的开始和结束 可以任意画，想画几个就画几个，想怎么连都可以，这也是个奇葩！ 只能呵呵哒，领导还放话了，工序中持续时间为0或-1的可以忽略，这又是个奇葩，这样来看，是不能用关键路径 的算法 来求的，可领导的意图就是关键路径，还让求什么工序最晚开始时间，工序的松弛时间，这些完全是关键路径 中所用到的概念，必须得用关键路径 的算法， 因为工序中存在持续时间为0和-1的节点，用关键路径的算法来做，是行不通的！！！ 我都怀疑领导是不是真的懂关键路径的一些概念，吧啦吧啦费了半天劲向领导解释关键路径的一些概念，他总算明白了点，最后决定只把耗时最长的一条或几条工序路径标记出来。这下好了，需求明确了，难度也不大，把图中从开始到结束间的所有可达路径遍历出来 ，然后找出累计持续时间最长一个或几个就行，解决方案如下 ：

1. 考虑到 MindFusion 画的节点中，节点与节点间的关系，简单的表示如下 ： A-->B  A-->C B-->E  C-->D D-->E,代码如下:

       private void StuffLinks(DataRow[] rows)
        {
            foreach (DataRow dr in rows)
            {
                //这是业务逻辑，获取工序节点的名称
                Model.DataSet_Config.PL_M_THRD_CFG_WORKRELATION2Row drRelation = dr as Model.DataSet_Config.PL_M_THRD_CFG_WORKRELATION2Row;
                // 连接名称
                string linkName = drRelation.I_PREWORK_ID.ToString() + "-" + drRelation.I_SUBWORK_ID.ToString();
                // hsLink 是哈稀表，用来保存工序节点间的连接， key: 连接名称 ， value: 连接对象
                if (!hsLink.Contains(linkName))
                {
                    // ShapeNode ,DiagramLink diagram  都是 MindFusion.Diagramming中的对象
                    // 前驱工序
                    ShapeNode preNode = (ShapeNode)hsNode[drRelation.I_PREWORK_ID];
                    // 后继工序
                    ShapeNode subNode = (ShapeNode)hsNode[drRelation.I_SUBWORK_ID];
                    // 工序间的连接
                    DiagramLink link = new DiagramLink(diagram, preNode, subNode);
                    // 连接的画笔
                    link.Pen = _Pen;
                    link.Tag = drRelation;
                    link.AutoRoute = false;
                    link.LayoutTraits[FlowLayoutTraits.LogicID] = "ControlFlow";
                    // 在图中添加连接，此时便会显示
                    diagram.Links.Add(link);
                    // 向哈稀表中添加  link 对象
                    hsLink.Add(linkName, link);
                }
            }
        }

2.  要遍历这些工序节点间的路径，涉及到有向图路径的相关知识， 有向图中顶点的存储方式有两种： 一、用邻接表结构 ；二、用矩阵 ；用矩阵来存储，遍历比较复杂，也很消耗资源，在此采用了 邻接表结构，建立的邻接表结构如下 ：

  /// <summary>
    /// AOV 网邻接表数据结构
    /// </summary>
    public class Vertex
    {
        /// <summary>
        /// 工序
        /// </summary>
        public DiagramNode Node { get; set; }
        /// <summary>
        /// 前驱节点
        /// </summary>
        public List<DiagramNode> PreNodes { get; set; }
        /// <summary>
        /// 后续节点
        /// </summary>
        public DiagramNode DesNodes { get; set; }
        /// <summary>
        /// 工序的耗时
        /// </summary>
        public decimal Weight { get; set; }
        /// <summary>
        /// 入度
        /// </summary>
        public int InDegree { get; set; }
        /// <summary>
        /// 出度
        /// </summary>
        public int OutDegree { get; set; }
    }

4.  通过工序节点来创建 AOV 网邻接表，为每一个节点设置入度和出度，用来区分是开始工序（只有出度没有入度）还是结束工序（只有入度没有出度），然后从结束节点开始向开始节点搜索（也可以从开始节点开始向结束节点搜索）具体代码如下：

    /// <summary>
        /// 获取关键路径
        /// </summary>
        private void GetCriticalPath()
        {
            // 原画笔颜色
            var originalPenBrush = new MindFusion.Drawing.SolidBrush(Color.FromArgb(, , ));
            // 原节点颜色
            var originalNodeBrush = new MindFusion.Drawing.LinearGradientBrush(Color.FromArgb(, , ), Color.FromArgb(, , ), );
            for (int i = ; i < stackCriticalPathLink.Count; i++)
            {
                DiagramLink item = stackCriticalPathLink.Pop();
                item.Pen = this._Pen;
                item.Brush = originalPenBrush;
                item.HeadPen = this._Pen;
            }

            foreach (var v in listAllPath)
            {
                foreach (var item in v)
                {
                    item.Node.Brush = originalNodeBrush;
                }
            }
            // 清空集合
            listAllPath.Clear();
            DiagramLinkCollection dlc = this.diagram.Links;
            if (dlc.Count == )
            {
                this.labelMsg.Text = "工序间未建立关系";
                return;
            }
            // AOV 网节点
            List<Vertex> listVertex = new List<Vertex>();
            // 构造AOV 网数据结构
            foreach (DiagramLink item in dlc)
            {
                var pre = item.Origin;
                var des = item.Destination;
                var vPre = listVertex.Find(p => p.Node.Equals(pre));
                if (vPre == null)
                {
                    vPre = new Vertex();
                    vPre.Node = pre;
                    vPre.Weight = GetWeight((NodeTagAtrribute)pre.Tag);
                    listVertex.Add(vPre);
                }
                var vDes = listVertex.Find(p => p.Node.Equals(des));
                if (vDes == null)
                {
                    vDes = new Vertex();
                    vDes.Node = des;
                    vDes.Weight = GetWeight((NodeTagAtrribute)des.Tag);
                    listVertex.Add(vDes);
                }
            }
            // 前驱工序,设置节点的出度,入度
            foreach (var item in listVertex)
            {
                GetPreNodes(item, dlc);
            }
            // 终止节点，出度为0的节点
            List<Vertex> listEnd = new List<Vertex>();
            GetStartEndNodes(dlc, listVertex, listEnd);
            // 全部路径
            GetAllPath(listVertex, listEnd);
            // 候选路径
            List<decimal> listWeights = new List<decimal>();
            foreach (var list in this.listAllPath)
            {
                decimal tempLength = list.Sum(p => p.Weight);
                listWeights.Add(tempLength);
            }
            // 关键路径
            decimal pathLenth = listWeights.Max();
            int num = ;
            for (int i = ; i < listWeights.Count; i++)
            {
                if (listWeights[i] == pathLenth)
                {
                    var temp = listAllPath[num];
                    listAllPath[num] = listAllPath[i];
                    listAllPath[i] = temp;
                    num++;
                }
            }
            int totalPath = this.listAllPath.Count();
            // 移除不是关键路径的项
            this.listAllPath.RemoveRange(num, listAllPath.Count() - num);
            // 关键路径节点,连线着色
            Color lineColor = Color.FromArgb(, , );
            Color nodeColor = Color.FromArgb(, , );
            var penLine = new MindFusion.Drawing.Pen(lineColor, 1.0F);
            var penBrush = new MindFusion.Drawing.SolidBrush(lineColor);
            var nodeBrush = new MindFusion.Drawing.LinearGradientBrush(nodeColor, nodeColor, );
            // 关键路径中的节点着色
            foreach (var item in listAllPath)
            {
                for (int i = , j = ; i < item.Count; i++)
                {
                    j = i + ;
                    var t = item[i];
                    if (j < item.Count)
                    {
                        var vertexDes = t.Node.Tag as NodeTagAtrribute;
                        var vertexrPre = item[j].Node.Tag as NodeTagAtrribute;
                        string key = vertexrPre._WorkOrder.I_ID.ToString() + "-" + vertexDes._WorkOrder.I_ID.ToString();
                        if (hsLink.Contains(key))
                        {
                            DiagramLink link = hsLink[key] as DiagramLink;
                            link.Pen = penLine;
                            link.Brush = penBrush;
                            link.HeadPen = penLine;
                            stackCriticalPathLink.Push(link);
                        }
                    }
                    t.Node.Brush = nodeBrush;
                }
            }
            if (totalPath > )
            {
                this.labelMsg.Text = string.Format("共 {0} 条路径,关键路径 {1} 条，长度：{2}(天)", totalPath, this.listAllPath.Count(), pathLenth);
            }
            else
            {
                this.labelMsg.Text = "工序间未建立关系";
            }

        }

        /// <summary>
        /// 前驱节点,同时设置AOV 网节点的入度,出度
        /// </summary>
        /// <param name="v"></param>
        /// <param name="dlc"></param>
        private void GetPreNodes(Vertex v, DiagramLinkCollection dlc)
        {
            v.PreNodes = new List<DiagramNode>();
            foreach (DiagramLink item in dlc)
            {
                if (v.Node.Equals(item.Destination))
                {
                    v.PreNodes.Add(item.Origin);
                    v.InDegree++;
                }
                if (v.Node.Equals(item.Origin))
                    v.OutDegree++;
            }
        }

        /// <summary>
        /// 获取起止节点
        /// </summary>
        /// <param name="dlc"></param>
        /// <param name="listVertexs"></param>
        /// <param name="listEnds"></param>
        private void GetStartEndNodes(DiagramLinkCollection dlc, List<Vertex> listVertexs, List<Vertex> listEnds)
        {
            foreach (var item in listVertexs)
            {
                if (item.OutDegree == )
                    listEnds.Add(item);
            }
        }

5. 节点路径 的搜索，这是本文要讲的关键，相关算法有：回溯法和非回溯法，具体代码如下：

        /// <summary>
        /// 在AOV 网结构中, 从结束节点开始,倒序搜索从结束节点到开始节点,所有的可达路径
        /// </summary>
        /// <param name="listVertex"></param>
        /// <param name="listEnd"></param>
        private void GetAllPath(List<Vertex> listVertex, List<Vertex> listEnd)
        {
            this.listAllPath.Clear();
            this.stackRecallVertex.Clear();
            for (int i = ; i < listEnd.Count; i++)
            {
                List<Vertex> listResult = new List<Vertex>();
                RecallSearchPath(listVertex, listEnd[i], listResult);
                //SearchPath(listVertex, listEnd[i]);
            }
        }

 5.1 回溯法

        /// <summary>
        /// 回溯搜索从结束节点到开始节点的所有可达路径
        /// </summary>
        /// <param name="listVertex"></param>
        /// <param name="vertex"></param>
        /// <param name="listResult"></param>
        private void RecallSearchPath(List<Vertex> listVertex, Vertex vertex, List<Vertex> listResult)
        {
            List<DiagramNode> preNodes = vertex.PreNodes;
            listResult.Add(vertex);
            // 没有前驱节点,即到达开始节点
            if (preNodes.Count == )
            {
                // 保存搜索的路径
                listAllPath.Add(listResult);
                // 回溯前判断
                if (this.stackRecallVertex.Count > )
                {
                    // 从栈顶弹出一个回溯点,并进行回溯
                    var vPre = this.stackRecallVertex.Pop();
                    var vDes = listVertex.Find(p => p.Node.Equals(vPre.DesNodes));
                    int index = listResult.IndexOf(vDes);
                    // 复制回溯点前的所有路径节点到新的集合
                    List<Vertex> listTemp = new List<Vertex>();
                    for (int i = ; i <= index; i++)
                    {
                        listTemp.Add(listResult[i]);
                    }
                    RecallSearchPath(listVertex, vPre, listTemp);
                }
            }
            if (preNodes.Count > )
            {
                // 有大于一个分支,将所有分支压入回溯栈,并从栈顶弹出一个分支进行搜索
                foreach (var item in preNodes)
                {
                    var v = listVertex.Find(p => p.Node.Equals(item));
                    v.DesNodes = vertex.Node;
                    this.stackRecallVertex.Push(v);
                }
                var vTop = this.stackRecallVertex.Pop();
                RecallSearchPath(listVertex, vTop, listResult);
            }
            if (preNodes.Count == )
            {
                // 没有分支,直接进行搜索遍历,直到开始节点
                var v = listVertex.Find(p => p.Node.Equals(preNodes[]));
                RecallSearchPath(listVertex, v, listResult);
            }
        }

5.2  非回溯法

  private void SearchPath(List<Vertex> listVertex, Vertex vertex)
        {
            // 栈,用于保存前驱顶点
            Stack<Vertex> stackVer = new Stack<Vertex>();
            // 保存一次完整搜索的顶点路径
            List<Vertex> listResult = new List<Vertex>();
            // 入栈
            stackVer.Push(vertex);
            while (stackVer.Count > )
            {
                // 从栈顶弹出一个顶点，以此顶点，开始搜索
                var vPre = stackVer.Pop();
                List<DiagramNode> preNodes = vPre.PreNodes;
                listResult.Add(vPre);
                if (preNodes.Count >= )
                {
                    // 前驱顶点有1个以上（即未到达开始顶点处）,将所有前驱顶点压入栈
                    foreach (var item in preNodes)
                    {
                        var v = listVertex.Find(p => p.Node.Equals(item));
                        v.DesNodes = vPre.Node;
                        stackVer.Push(v);
                    }
                }
                else
                {
                    // 没有前驱顶点，即搜索到达开始顶点处，将本次搜索的完整路径保存下来
                    // 保存搜索的路径
                    listAllPath.Add(listResult);
                    // 判断栈内顶点数，若不为空， 获取栈的头部顶点的后继顶点的索引，并从索引0开复制到此索引处的顶点
                    if (stackVer.Count > )
                    {
                        var vDes = listVertex.Find(p => p.Node.Equals(stackVer.Peek().DesNodes));
                        int index = listResult.IndexOf(vDes);
                        // 从索引0开复制到此索引处的顶点
                        List<Vertex> listTemp = new List<Vertex>();
                        for (int i = ; i <= index; i++)
                        {
                            listTemp.Add(listResult[i]);
                        }
                        // 更新搜索路径中的顶点
                        listResult = listTemp;
                    }
                }
            }

        }

6. 运行效果

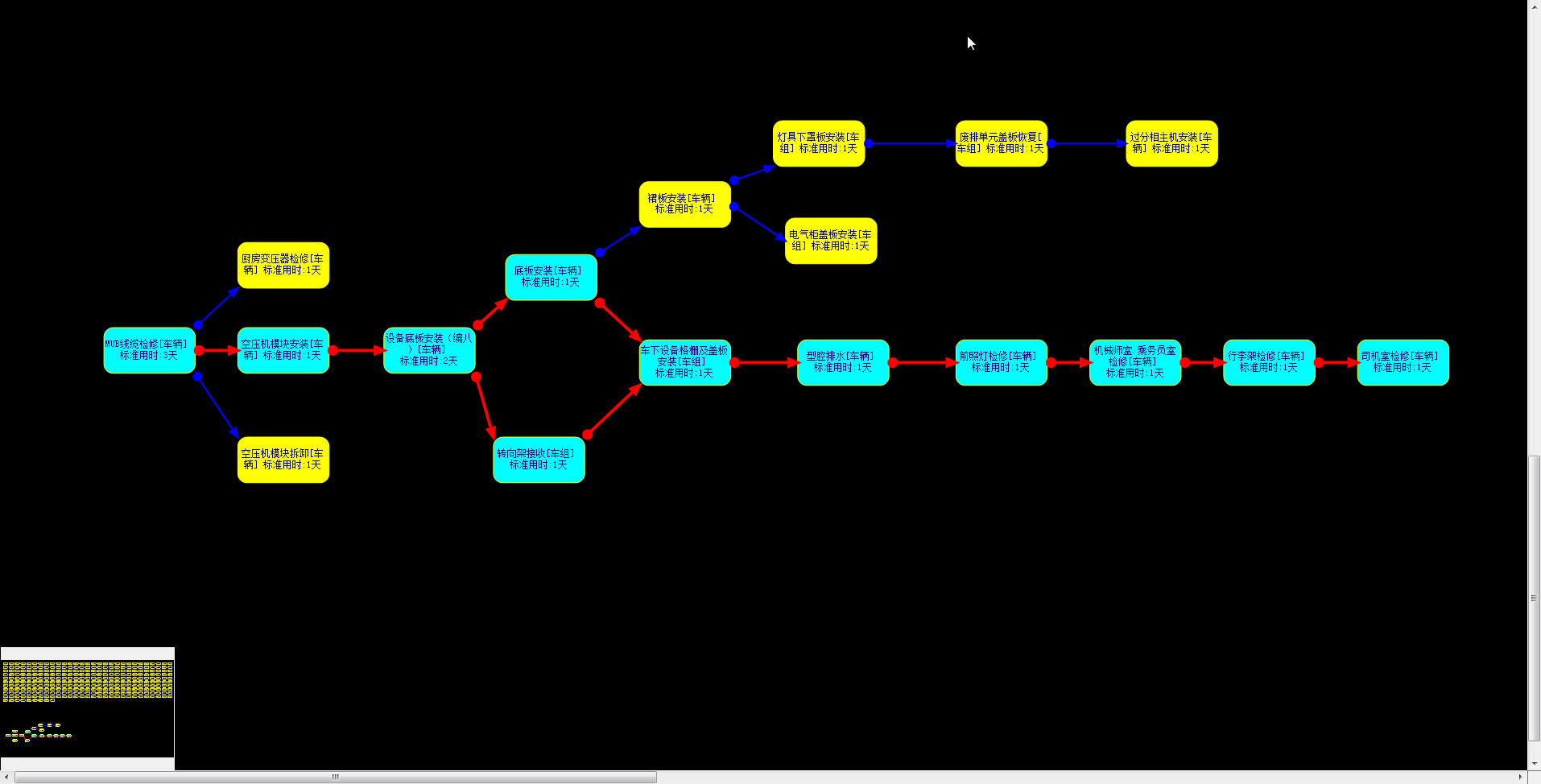
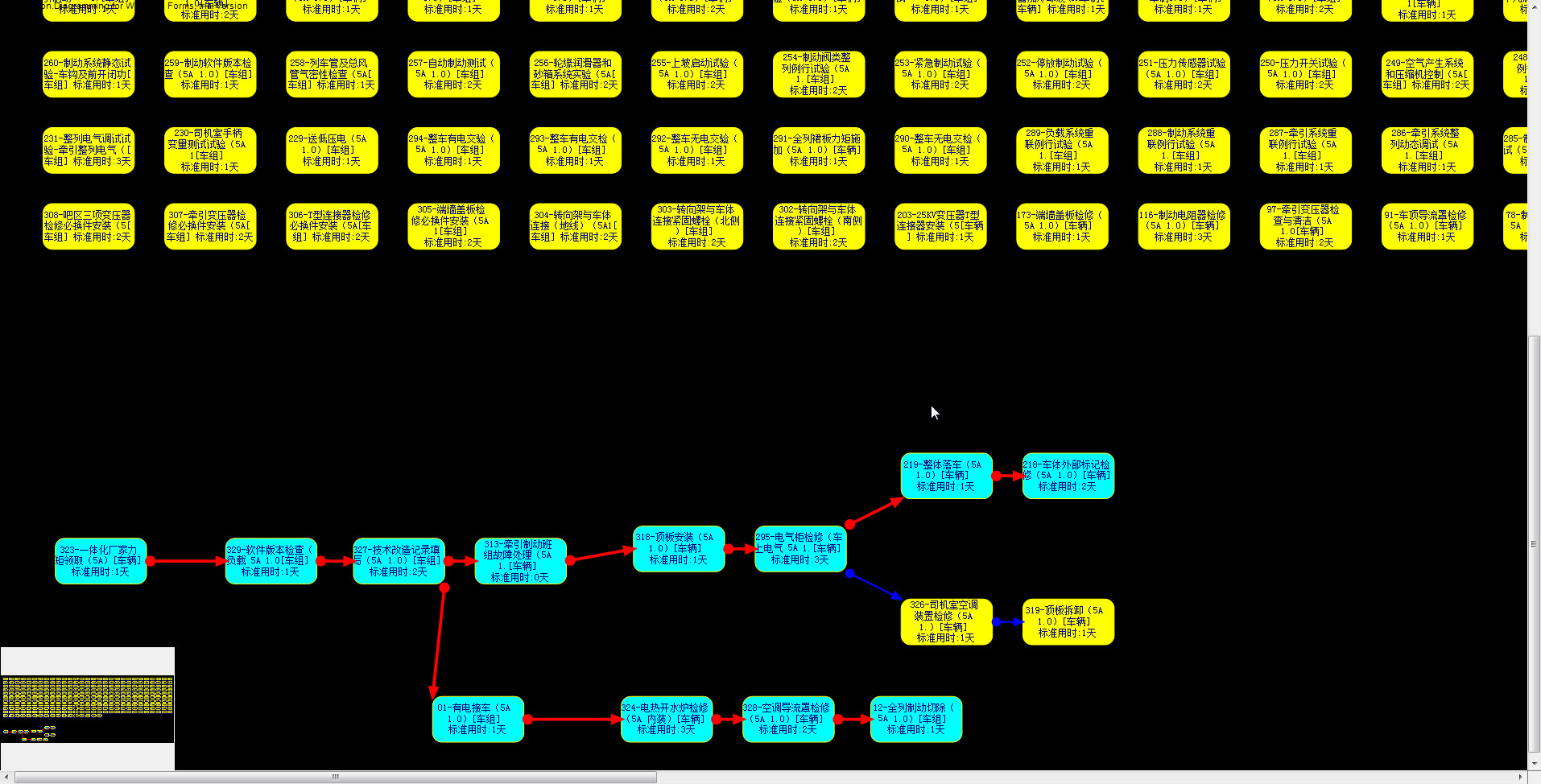
相关资料：

MindFusion官网组件：https://www.mindfusion.eu/winforms-ui-dock-control.html

MindFusion 官网API 文档：https://www.mindfusion.eu/onlinehelp/flowchartnet/index.htm

关键路径算法：https://www.jianshu.com/p/1857ed4d8128

回溯算法：https://zh.wikipedia.org/wiki/%E5%9B%9E%E6%BA%AF%E6%B3%95

AOV 网：http://www.cnblogs.com/KennyRom/p/6120039.html