实现prim算法

如下找出该图的最小生成树

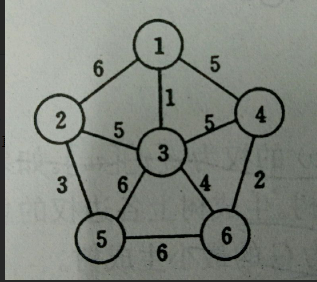
prim算法是求解该类问题的一种经典算法

Prim算法的基本思路：
将图中的所有的顶点分为两类：树顶点（已经被选入生成树的顶点）和非树顶点（还未被选入生成树的顶点）。首先选择任意一个顶点加入生成树，接下来要找出一条边添加到生成树，

这需要枚举每一个树顶点到每一个非树顶点所有的边，然后找到最短边加入到生成树。依次，重复操作n-1次，直到将所有顶点都加入生成树中。

算法实现如下

 #include<bits/stdc++.h>
 using namespace std;
 void Prim(int n,int c[ ][])
 {
     int  lowcost[];//各非树顶点到树顶点集的最短路径
     int closet[];//非树顶点到树顶点集的最小边中相对的顶点
     bool foot[n+];//表示是否已经为树顶点，初始为false
     memset(lowcost,,sizeof(lowcost));
     memset(closet,,sizeof(closet));
     foot[]=true;//假设先把1作为初始顶点
     for(int i=;i<=n;i++){//假设从节点一开始
         foot[i]=false;
         closet[i]=;
         lowcost[i]=c[][i];
     }
     for(int i=;i<n;i++){
         int  min=;
         int j=;
         for(int k=;k<=n;k++){//计算非树顶点到树顶点集的最短路径，并把对应顶点记为j
             if((lowcost[k]<min)&&(foot[k]==false)){
                 min=lowcost[k];
                 j=k;
             }
         }
         cout <<"选边"<< "("<<closet[j] << "," <<j<<")" << endl;//把改变归为已选边，并把foot[j]设为true
         foot[j]=true;
         for(int k=;k<=n;k++){//由于新的顶点加入树顶点，所以要更新非树顶点到树顶点集的最短路径lowcost[j]，和对应的clost[j]
             if((c[j][k]<lowcost[k])&&(foot[k]==false)){
                 lowcost[k]=c[j][k];
                 closet[k]=j;
             }
         }
     }

 }
 int main()
 {
     cout << "请输入图的顶点数" << endl;
     int n;
     cin >>n;
     cout << "请输入图的边数" << endl;
     int m;
     cin >> m;
     cout << "请输入图的边的两个端点和边的长度" << endl;
     int c[][];
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++){
             c[i][j]=;
         }
     }
     int i1,j,k;
     for(int i=;i<=m;i++){
         cin >>i1 >> j >> k;
         c[i1][j]=k;
         c[j][i1]=k;
     }
     Prim(n,c);
     return ;

 }

运行结果如下