PCA与KPCA

PCA是利用特征的协方差矩阵判断变量间的方差一致性，寻找出变量之间的最佳的线性组合，来代替特征，从而达到降维的目的，但从其定义和计算方式中就可以看出，这是一种线性降维的方法，如果特征之间的关系是非线性的，用线性关系去刻画他们就会显得低效，KPCA正是应此而生，KPCA利用核化的思想，将样本的空间映射到更高维度的空间，再利用这个更高的维度空间进行线性降维。

如果样本的维度是k，样本个数是n（n>k），那么首先需要将样本投射到n维空间，这个n维空间是这样计算的：首先计算n个样本间的距离矩阵D（n*n），核函数F，则F(D)就是他的高维空间投射。

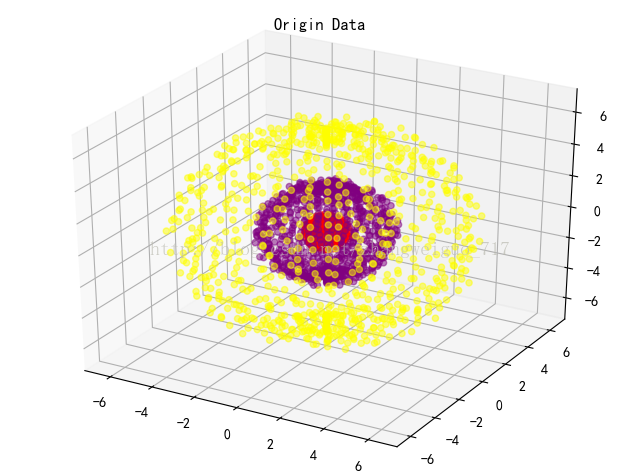
我们用几个例子来看KPCA与PCA的不同：我们用三维空间中三个同心球面来作为三类原始数据，用不同的核函数来将其降维到二维平面，当核函数是linear（线性）时，就是PCA，其他的核函数，如RBF，SIGMOID，多项式等，都是非常常用的核化函数。

原始数据分布点如下，共2700个样本，每一类样本900个：

用KPCA各类核函数将其降维后，达到效果如下：

很明显，RBF核能将不同类别的数据分开，而PCA只是将其做了一个投影，在这里，由于三个球是相互嵌套的，很难找到合适的投影方向，将三类数据很好的分开，由此造成了非常差的表现，KPCA的优点由此可见。