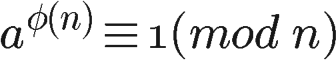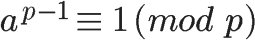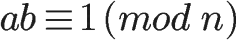RSA加密算法详解(一)

如果你问我，哪一种算法最重要？

　　我可能会回答"公钥加密算法"。

　　因为它是计算机通信安全的基石，保证了加密数据不会被破解。你可以想象一下，信用卡交易被破解的后果。

　　进入正题之前，我先简单介绍一下，什么是"公钥加密算法"。

　　一、一点历史

　　1976 年以前，所有的加密方法都是同一种模式：

（1）甲方选择某一种加密规则，对信息进行加密；

（2）乙方使用同一种规则，对信息进行解密。

　　由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-key algorithm）。

　　这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

　　1976 年，两位美国计算机学家 Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为"Diffie-Hellman 密钥交换算法"。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

　　这种新的加密模式被称为"非对称加密算法"。

（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。

（2）甲方获取乙方的公钥，然后用它对信息加密。

（3）乙方得到加密后的信息，用私钥解密。

　　如果公钥加密的信息只有用私钥解开，那么只要私钥不泄漏，通信就是安全的。

　　1977 年，三位数学家 Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做 RSA 算法。从那时直到现在，RSA 算法一直是最广为使用的"非对称加密算法"。毫不夸张地说，只要有计算机网络的地方，就有 RSA 算法。

　　这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长 RSA 密钥是 768 个二进制位。也就是说，长度超过 768 位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024 位的 RSA 密钥基本安全，2048 位的密钥极其安全。

　　下面，我就进入正题，解释 RSA 算法的原理。文章共分成两部分，今天是第一部分，介绍要用到的四个数学概念。你可以看到，RSA 算法并不难，只需要一点数论知识就可以理解。

　　二、互质关系

　　如果两个正整数，除了 1 以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15 和 32 没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

　　关于互质关系，不难得到以下结论：

1. 任意两个质数构成互质关系，比如 13 和 61。

2. 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如 3 和 10。

3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如 97 和 57。

4. 1 和任意一个自然数是都是互质关系，比如 1 和 99。

5. p 是大于 1 的整数，则p和p-1 构成互质关系，比如 57 和 56。

6. p 是大于 1 的奇数，则p和p-2 构成互质关系，比如 17 和 15。

　　三、欧拉函数

　　请思考以下问题：

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在 1 到 8 之中，有多少个数与 8 构成互质关系？）

　　计算这个值的方法就叫做欧拉函数，以φ(n)表示。在 1 到 8 之中，与 8 形成互质关系的是1、3、5、7，所以 φ(n) = 4。

　　φ(n) 的计算方法并不复杂，但是为了得到最后那个公式，需要一步步讨论。

　　第一种情况

　　如果n=1，则 φ(1) = 1 。因为 1 与任何数（包括自身）都构成互质关系。

　　第二种情况

　　如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如 5 与1、2、3、4 都构成互质关系。

　　第三种情况

　　如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于 1 的整数)，则

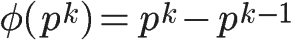
　　比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。

　　这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1) 个，即1×p、2×p、3×p、...、p^(k-1)×p，把它们去除，剩下的就是与n互质的数。

　　上面的式子还可以写成下面的形式：

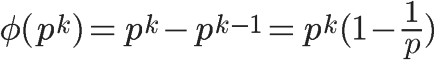
　　第四种情况

　　如果n可以分解成两个互质的整数之积，

n = p1 × p2

　　则

φ(n) = φ(p1p2) = φ(p1)φ(p2)

　　即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

　　这一条的证明简单说是这样的：如果a与 p1 互质(a<p1)，b与 p2 互质(b<p2)，则 a×p2+b×p1 肯定与 p1p2 互质。由于a一共有φ(p1) 种取值可能，b一共有φ(p2) 个取值可能，所以φ(p1p2) 就等于φ(p1)φ(p2)。

　　第五种情况

　　因为任意一个大于 1 的正整数，都可以写成一系列质数的积。

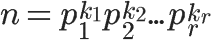
　　根据第 4 条的结论，得到

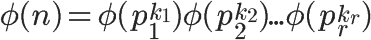
　　再根据第 3 条的结论，得到

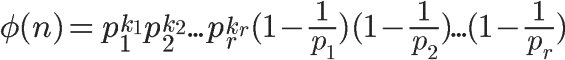
　　也就等于

　　这就是欧拉函数的通用计算公式。比如，1323 的欧拉函数，计算过程如下：

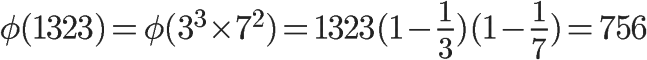
　　四、欧拉定理

　　欧拉函数的用处，在于欧拉定理。"欧拉定理"指的是：

如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

　　也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3 和 7 互质，而 7 的欧拉函数φ(7) 等于6，所以 3 的 6 次方（729）减去1，可以被 7 整除（728/7=104）。

　　欧拉定理的证明比较复杂，这里就省略了。我们只要记住它的结论就行了。

　　欧拉定理可以大大简化某些运算。比如，7 和 10 互质，根据欧拉定理，

　　已知 φ(10) 等于4，所以马上得到 7 的 4 倍数次方的个位数肯定是1。

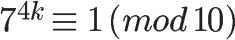
　　因此，7 的任意次方的个位数（例如 7 的 222 次方），心算就可以算出来。

　　欧拉定理有一个特殊情况。

假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

　　这就是著名的费马小定理。它是欧拉定理的特例。

　　欧拉定理是 RSA 算法的核心。理解了这个定理，就可以理解 RSA。

　　五、模反元素

　　还剩下最后一个概念：

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说 ab 被n除的余数是1。

这时，b就叫做a的"模反元素"。

　　比如，3 和 11 互质，那么 3 的模反元素就是4，因为 (3 × 4)-1 可以被 11 整除。显然，模反元素不止一个， 4 加减 11 的整数倍都是 3 的模反元素 {...，-18,-7,4,15,26,...}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

　　欧拉定理可以用来证明模反元素必然存在。

　　可以看到，a的 φ(n)-1 次方，就是a的模反元素。