POJ 2676 Sudoku (数独 DFS)
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 14368 | Accepted: 7102 | Special Judge | ||
Description
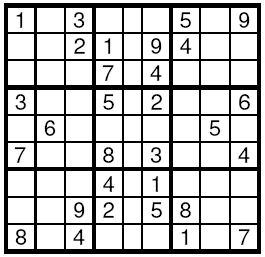
Input
Output
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
#include <cstdio>
char s[];
int num[][];
bool flag; bool ok(int n, int cur)
{
int r = n / ; //当前行
int c = n % ; //当前列
for(int j = ; j < ; j++) //枚举列
if (num[r][j] == cur)
return false;
for(int i = ; i < ; i++) //枚举行
if (num[i][c] == cur)
return false;
//得到当前所在的子矩阵的第一个元素位置
int x = r / * ;
int y = c / * ;
//枚举子矩阵中的元素
for(int i = x; i < x + ; i++)
for(int j = y; j < y + ; j++)
if (num[i][j] == cur)
return false;
return true;
} void DFS(int n)
{
if(n > || flag)
{
flag = true;
return;
}
if(num[n / ][n % ])//当前位置有数字直接搜索下一位
{
DFS(n + );
if(flag)
return;
}
else
{
for(int cur = ; cur <= ; cur++) //枚举数字
{
if(ok(n, cur)) //若ok则插入
{
num[n / ][n % ] = cur;
DFS(n + );
if(flag)
return;
num[n / ][n % ] = ; //还原
}
}
}
} int main()
{
int T;
scanf("%d", &T);
while(T--)
{
flag = false;
for(int i = ; i < ; i++) //得到数独矩阵
{
scanf("%s", s);
for(int j = ; j < ; j++)
num[i][j] = (s[j] - '');
}
DFS(); //从第一位开始搜
for(int i = ; i < ; i++)
{
for(int j = ; j < ; j++)
printf("%d", num[i][j]);
printf("\n");
}
}
}
题解来源:http://blog.csdn.net/tc_to_top/article/details/43699047
POJ 2676 Sudoku (数独 DFS)的更多相关文章
- POJ - 2676 Sudoku 数独游戏 dfs神奇的反搜
Sudoku Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smalle ...
- POJ 2676 Sudoku (DFS)
Sudoku Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 11694 Accepted: 5812 Special ...
- 深搜+回溯 POJ 2676 Sudoku
POJ 2676 Sudoku Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 17627 Accepted: 8538 ...
- ACM : POJ 2676 SudoKu DFS - 数独
SudoKu Time Limit:2000MS Memory Limit:65536KB 64bit IO Format:%lld & %llu POJ 2676 Descr ...
- POJ 2676 - Sudoku - [蓝桥杯 数独][DFS]
题目链接:http://poj.org/problem?id=2676 Time Limit: 2000MS Memory Limit: 65536K Description Sudoku is a ...
- 搜索 --- 数独求解 POJ 2676 Sudoku
Sudoku Problem's Link: http://poj.org/problem?id=2676 Mean: 略 analyse: 记录所有空位置,判断当前空位置是否可以填某个数,然后直 ...
- poj 2676 Sudoku ( dfs )
dfs 用的还是不行啊,做题还是得看别人的博客!!! 题目:http://poj.org/problem?id=2676 题意:把一个9行9列的网格,再细分为9个3*3的子网格,要求每行.每列.每个子 ...
- DFS POJ 2676 Sudoku
题目传送门 题意:数独问题,每行每列以及每块都有1~9的数字 分析:一个一个遍历会很慢.先将0的位子用vector存起来,然后用rflag[i][num] = 1 / 0表示在第i行数字num是否出现 ...
- POJ 2676/2918 数独(dfs)
思路:记录每行每列每一个宫已经出现的数字就可以.数据比較弱 另外POJ 3074 3076 必须用剪枝策略.但实现较麻烦,还是以后学了DLX再来做吧 //Accepted 160K 0MS #incl ...
随机推荐
- serializeArray()与 serialize()
serialize()序列表表格内容为字符串,用于 Ajax 请求. serializeArray()序列化表格元素 (类似 '.serialize()' 方法) 返回 JSON 数据结构数据. .s ...
- 【Codeforces】【#295】【Div.1】
嘛,一直以来蒟蒻都没怎么打过CF……现在还是蓝名狗……今天跟着zyf打了一场virtual,果断一题滚粗
- Java与C/C++的比较(转)
原文链接:Java和c++比较 总结一下Java的小知识,只是想稍微提醒一下自己这些基础的东西,放在这里,随时可以阅览和添加一下,以免走错了方向. 1.面向对象程序设计 面向对象程序设计语言可以直观的 ...
- 对于DQN的三大改进 - 这篇讲的好些
可以看这篇文章: https://blog.csdn.net/u013236946/article/details/73161586 这篇也讲的不错: https://www.cnblogs.com/ ...
- 附1 踩过的jedis的一些坑
1.java.lang.Long to java.lang.B]类型转换异常 解决方案:归还资源部分,使用jedis.close() 2.jedis数组越界异常 解决方案:版本太低,升到2.8.0
- Sharepoint2013 列表的NewForm 页面添加一个 保存新建 按钮
昨天一同事问我如何在sharepoint2013的NewForm.aspx页面上添加一个 save and new的button.实现save 和new的功能,save的功能和默认的save按钮效果一 ...
- [Algorithm] Inorder Successor in a binary search tree
For the given tree, in order traverse is: visit left side root visit right side // 6,8,10,11,12,15,1 ...
- php代码收集
thinkphp <?php class HekaAction extends BaseAction{ public function index(){ require_once './wang ...
- jdbc:initialize-database标签的研究
在spring的applicationContext.xml中如果引入了:<?xml version="1.0" encoding="UTF-8"?> ...
- 微信小程序 - 上传图片(组件)
更新日期: 2019/3/14:首次发布,更新了2018/12/30的UI以及反馈信息获取方式,具体请下载:demo. 2019/3/20:感谢544429676@qq.com指出的现存bug,已修复 ...
