Deep Learning基础--随时间反向传播 （BackPropagation Through Time，BPTT）推导

1. 随时间反向传播BPTT（BackPropagation Through Time, BPTT）

RNN（循环神经网络）是一种具有长时记忆能力的神经网络模型，被广泛用于序列标注问题。一个典型的RNN结构图如下所示：

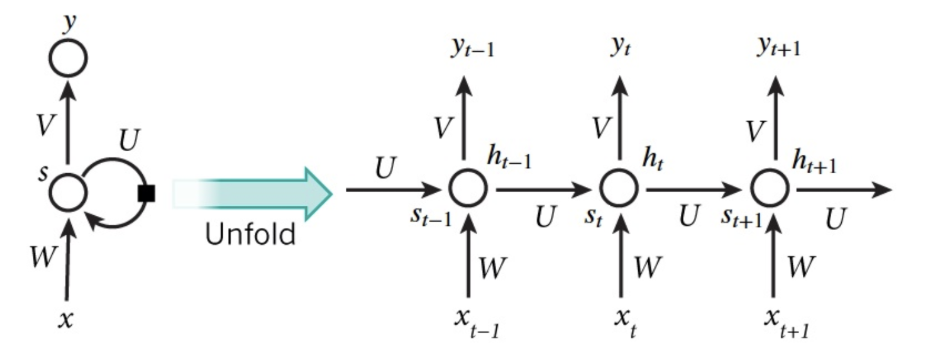
从图中可以看到，一个RNN通常由三小层组成，分别是输入层、隐藏层和输出层。与一般的神经网络不同的是，RNN的隐藏层存在一条有向反馈边，正是这种反馈机制赋予了RNN记忆能力。要理解左边的图可能有点难度，我们将其展开成右边的这种更加直观的形式，其中RNN的每个神经元接受当前时刻的输入$x_t$以及上一时刻隐单元的输出$s_{t-1}$，计算出当前神经元的输入$s_t$。三个权重矩阵$U$, $V$和$W$就是要通过梯度下降来拟合的参数。整个优化过程叫做BPTT（BackPropagation Through Time, BPTT）。

形式化如下：

$$ { s }_{ t }=\tanh  \left( U{ x }_{ t }+W{ s }_{ t-1 } \right) \\ { \hat { y }  }_{ t }=softmax\left( V{ s }_{ t } \right)   \tag{1}$$

同样地，定义交叉熵损失函数如下：

$$ { E }_{ t }\left( { y }_{ t },{ \hat { y }  }_{ t } \right) =-{ y }_{ t }log{ \hat { y }  }_{ t }\\ { E\left( y,\hat { y }  \right)  }=\sum _{ t }^{  }{ { E }_{ t }\left( { y }_{ t },{ \hat { y }  }_{ t } \right)  } \\ =-\sum _{ t }^{  }{ { y }_{ t }log{ \hat { y }  }_{ t } }   \tag{2}$$

下面我们将举个具体的例子。

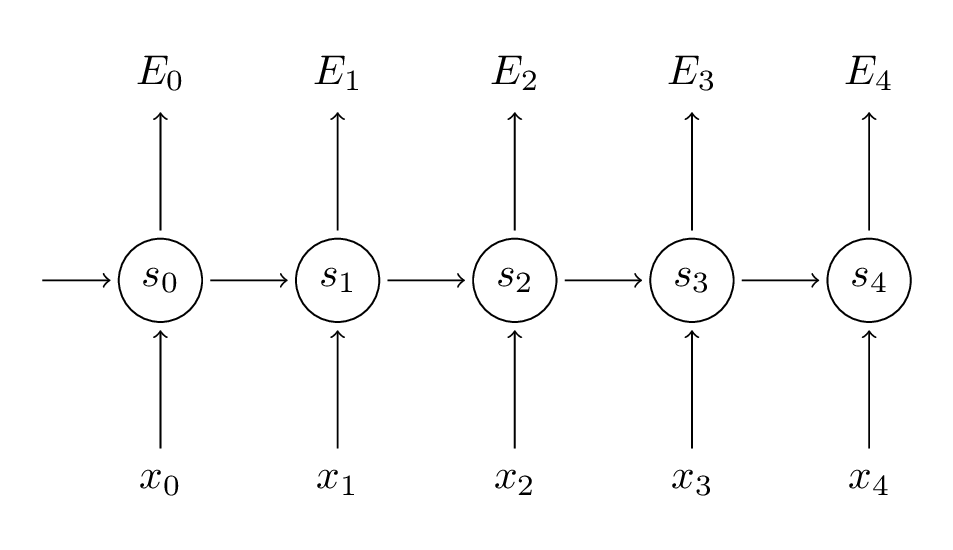
我们的目标是通过梯度下降来拟合参数矩阵$U$, $V$和$W$。如同求损失时的加和，有$\frac { \partial E }{ \partial W } =\sum _{ t }^{  }{ \frac { \partial { E }_{ t } }{ \partial W }  } $。

为了计算这些梯度，我们使用链式法则。我们将以$E_3$为例，做如下推导。

$$  \frac { \partial { E }_{ 3 } }{ \partial V } =\frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial V } \\ =\frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial { z }_{ 3 } } \frac { \partial { z }_{ 3 } }{ \partial V } \\ =\left( { \hat { y }  }_{ 3 }-{ y }_{ 3 } \right) \otimes { s }_{ 3 } \tag{3}$$

在上面式子中，$z_3=V s_3$，$\otimes$表示两个向量的外积。对$V$的偏导是简单的，因为$t=3$时间步的对$V$的偏导只与${ \hat { y }  }_{ 3 }$，$y_3$和$s_3$有关。但是，对于$\frac { \partial { E }_{ 3 } }{ \partial W }$就没有这么简单了，如图：

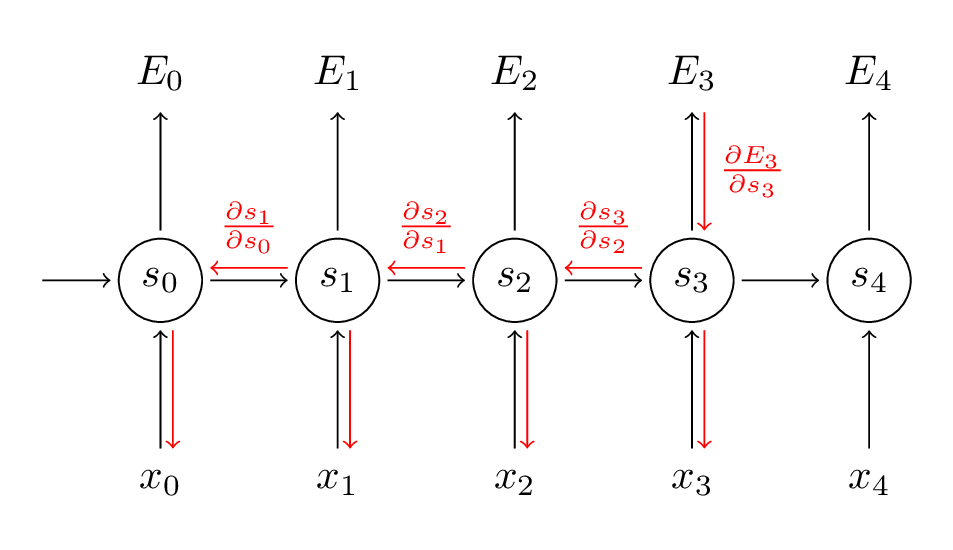
推导过程如下：

$$   \frac { \partial { E }_{ 3 } }{ \partial W } =\frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial { s }_{ 3 } } \frac { \partial { s }_{ 3 } }{ \partial W } \\ =\sum _{ k=0 }^{ 3 }{ \frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial { s }_{ 3 } } \frac { \partial { s }_{ 3 } }{ \partial { s }_{ k } } \frac { \partial { s }_{ k } }{ \partial W }  }  \tag{4}   $$

上式中，我们可以看到，这与标准的BP算法并无太多不同，唯一的区别在于需要对各时间步求和。这也是标准RNN难以训练的原因：序列（句子）可能很长，可能是20个字或更多，因此需要反向传播多个层。在实践中，许多人将时间步进行截断来控制传播层数。

BPTT实现的代码如下：

def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation: dL/dz
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            # Add to gradients at each previous step
            dLdW += np.outer(delta_t, s[bptt_step-1])
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step dL/dz at t-1
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return [dLdU, dLdV, dLdW]

2. 梯度消失问题

标准RNN难以学习到文本的上下文依赖，例如“The man who wore a wig on his head went inside”，句子要表达的是带着假发的男人进去了而不是假发进去了，这一点对于标准RNN的训练很难。为了理解这个问题，我们先看看上面的式子：

$$ \frac { \partial { E }_{ 3 } }{ \partial W } =\sum _{ k=0 }^{ 3 }{ \frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial { s }_{ 3 } } \frac { \partial { s }_{ 3 } }{ \partial { s }_{ k } } \frac { \partial { s }_{ k } }{ \partial W }  }   \tag{5}$$

注意，其中的$\frac { \partial { s }_{ 3 } }{ \partial { s }_{ k } } $仍然包含着链式法则，例如$\frac { \partial { s }_{ 3 } }{ \partial { s }_{ 1 } } =\frac { \partial { s }_{ 3 } }{ \partial { s }_{ 2 } } \frac { \partial { s }_{ 2 } }{ \partial { s }_{ 1 } } $。

所以上面的式子（5）可以重写为式子（6）,即逐点导数的雅克比矩阵：

$$  \frac { \partial { E }_{ 3 } }{ \partial W } =\sum _{ k=0 }^{ 3 }{ \frac { \partial { E }_{ 3 } }{ \partial { \hat { y }  }_{ 3 } } \frac { \partial { \hat { y }  }_{ 3 } }{ \partial { s }_{ 3 } } \left( \prod _{ j=k+1 }^{ 3 }{ \frac { \partial { s }_{ j } }{ \partial { s }_{ j-1 } }  }  \right) \frac { \partial { s }_{ k } }{ \partial W }  }   \tag{6} $$

而tanh函数和其导数图像如下：

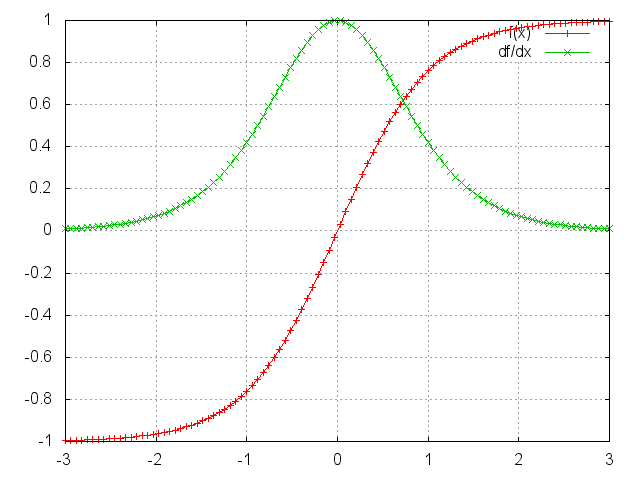
可见，tanh函数（sigmoid函数也不例外）的两端都有接近0的导数。当出现这种情况时，我们认为相应的神经元已经饱和。参数矩阵将以指数方式快速收敛到0，最终在几个时间步后完全消失。来自“遥远”的时间步的权重迅速为0，从而不会对现在的学习状态产生贡献：学不到远处上下文依赖。

很容易想象，根据我们的激活函数和网络参数，如果雅可比矩阵的值很大，将会产生梯度爆炸。首先，梯度爆炸是显而易见的，权重将渐变为NaN（不是数字），程序将崩溃。其次，将梯度剪切到预定义的阈值是一种非常简单有效的梯度爆炸解决方案。当然，梯度消失问题影响更加恶劣，因为要知道它们何时发生或如何处理它们并不简单。

目前，已经有几种方法可以解决梯度消失问题。正确初始化$W$矩阵可以减少消失梯度的影响。正规化也是如此。更优选的解决方案是使用Relu代替tanh或S形激活函数。ReLU导数是0或1的常数，因此不太可能遇到梯度消失。更流行的解决方案是使用长短期记忆单元（LSTM）或门控循环单元（GRU）架构。LSTM最初是在1997年提出的，也是今天NLP中使用最广泛的模型。GRU，最初于2014年提出，是LSTM的简化版本。这两种RNN架构都明确地设计用于处理梯度消失并有效地学习远程依赖性。

参考英文博客：http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/