【BZOJ】4766: 文艺计算姬

【题目】给定两边节点数为n和m的完全二分图，求生成树数取模给定的p。n,m,p<=10^18。

【算法】生成树计数（矩阵树定理）

【题解】参考自 [bzoj4766]文艺计算姬 by WerKeyTom_FTD

构造完全二分图的基尔霍夫矩阵的余子式如下（去除第一行第一列）：n=3,m=3，空白格皆为0

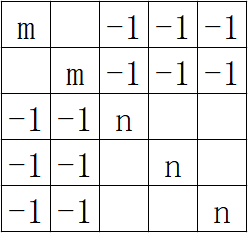
为了消项形成倒三角，将所有其它n+m-1行全部加到第n行上，则有：

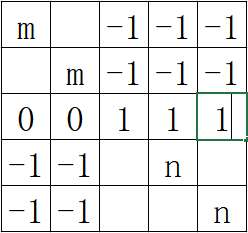
然后将第n行叠加到前面n-1行上，形成倒三角：

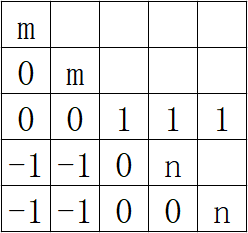
虽然不是完全的倒三角，但因为其它排列的积为0所以没有影响，那么主对角线上的乘积就是答案。

ans=n^(m-1)*m^(n-1)

#include<cstdio>
#define ll long long
ll n,m,MOD;
ll mul(ll x,ll k){
    ll ans=;x%=MOD;
    while(k){
        if(k&)ans=(ans+x)%MOD;
        x=(x+x)%MOD;
        k>>=;
    }
    return ans;
}
ll power(ll x,ll k){
     ll ans=;
     while(k){
         if(k&)ans=mul(ans,x);
         x=mul(x,x);
         k>>=;
     }
     return ans;
}
int main(){
    scanf("%lld%lld%lld",&n,&m,&MOD);
    printf("%lld",mul(power(n,m-),power(m,n-)));
    return ;
}

全程long long的运算必须快速乘+快速幂。