[ML学习笔记] 回归分析(Regression Analysis)
[ML学习笔记] 回归分析(Regression Analysis)
回归分析:在一系列已知自变量与因变量之间相关关系的基础上,建立变量之间的回归方程,把回归方程作为算法模型,实现对新自变量得出因变量的关系。
回归与分类的区别:回归预测的是连续变量(数值),分类预测的是离散变量(类别)。
线性回归
线性回归通过大量的训练出一个与数据拟合效果最好的模型,实质就是求解出每个特征自变量的权值θ。
设有特征值x1、x2(二维),预测值 $ h_\theta(x)=\theta_0 + \theta_1x_1 + \theta_2x_2 $。将其写为矩阵形式:令x0为全为1的向量,则预测值 $ h_\theta(x)=\sum_{i=0}^n\theta_i x_i =\theta^T x$。
真实值和预测值之间的偏差用 \(\varepsilon\) 表示,则有预测值 $ y^{(i)} = \theta^Tx^{(i)} + \varepsilon^{(i)}$。
假设误差\(\varepsilon^{(i)}\)是独立同分布的(通常认为服从均值为 \(0\) 方差为 \(\sigma^2\) 的正态分布),有:
\[
\begin{split}
&p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(\epsilon^{(i)})^2}{2\sigma^2}} \\
代入则有&p(y^{(i)}\mid x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \\
\end{split}
\]
符号解释
p(x|theta)表示条件概率,是随机变量
p(x;theta)表示待估参数(固定的,只是当前未知),可直接认为是p(x),加了分号是为了说明这里有个theta参数
上式用语言描述就是,要取一个怎样的\(\theta\),能够使得在\(x^{(i)}\)的条件下最有可能取到\(y^{(i)}\)。
可用极大似然估计求解,
\[
L(\theta)=\prod_{i=1}^mp(y^{(i)}\mid x^{(i)};\theta)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}}
\]
\[
\begin{split}
l(\theta)&=\log L(\theta)\\
&=\log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \\
&= \sum_{i=1}^m\log\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \\
&= m\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{2\sigma^2}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2\\
\end{split}
\]
化为求目标函数\(J(\theta)=\dfrac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2\)的最小值。
最小二乘法求解
用矩阵形式表示:
\[
J(\theta)=\frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2
=\frac{1}{2}(X\theta-y)^T(X\theta-y)
\]
然后对\(\theta\)求导:
\[
\begin{split}
\triangledown_\theta J(\theta)&=\triangledown_\theta(\frac{1}{2}(X\theta-y)^T(X\theta-y))\\
&=\triangledown_\theta(\frac{1}{2}(\theta^TX^T-y^T)(X\theta-y))\\
&=\triangledown_\theta(\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty))\\
&=\frac{1}{2}(2X^TX\theta-X^Ty-(y^TX)^T)\\
&=X^TX\theta-X^Ty
\end{split}
\]
令 \(X^TX\theta-X^Ty=0\),则有最终结果 \(\theta = (X^TX)^{-1}X^Ty\)
梯度下降法求解
上述方法有时候会出现不能直接求出极值的情况,比如矩阵不可逆,只能通过不断优化的过程求解。梯度下降顾名思义,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的方向,就能让函数值下降的最快。
设 \(h_\theta(x)=\theta_1x+\theta_0\),
\[
\begin{split}
J(\theta_0,\theta_1)&=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2\\
\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})\\
\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})x_i\\
\end{split}
\]
更新后的\(\theta_0,\theta_1\)(选取合适的\(\alpha\)做步长):
\[
\begin{split}
\theta_0:=\theta_0-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0}\\
\theta_1:=\theta_1-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1}
\end{split}
\]
逻辑回归(二分类问题)
逻辑回归本质不是回归,而是分类。可用Sigmoid函数 \(g(x) = \dfrac{1}{1+e^{-x}}\)将任意实数x映射到(0,1)区间从而进行类别划分,一般默认概率大于等于0.5则为1,小于0.5则为0,也可以自行设置阈值。
用一句话来说就是:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数得出分类概率,通过阈值过滤来达到将数据二分类的目的。
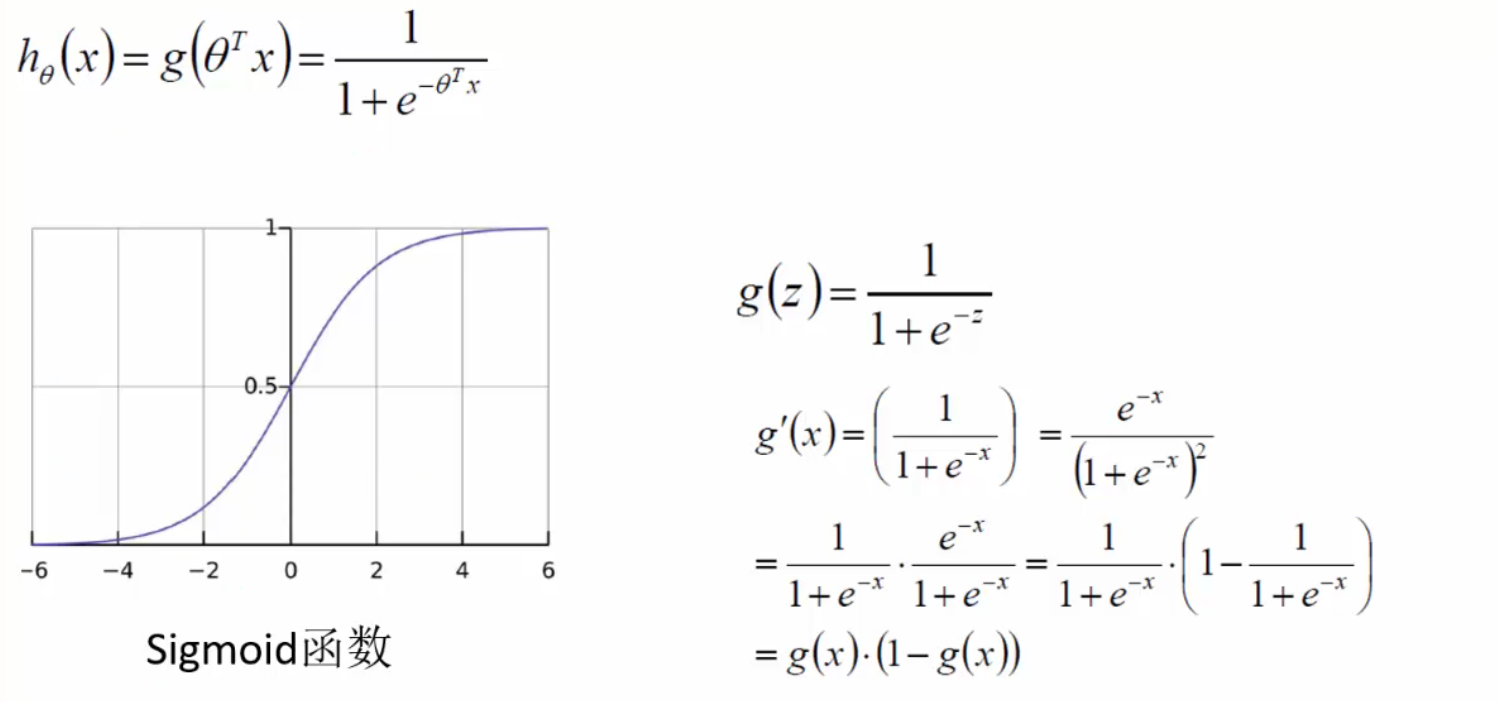
[ML学习笔记] 回归分析(Regression Analysis)的更多相关文章
- [Machine Learning]学习笔记-Logistic Regression
[Machine Learning]学习笔记-Logistic Regression 模型-二分类任务 Logistic regression,亦称logtic regression,翻译为" ...
- [ML学习笔记] XGBoost算法
[ML学习笔记] XGBoost算法 回归树 决策树可用于分类和回归,分类的结果是离散值(类别),回归的结果是连续值(数值),但本质都是特征(feature)到结果/标签(label)之间的映射. 这 ...
- [ML学习笔记] 朴素贝叶斯算法(Naive Bayesian)
[ML学习笔记] 朴素贝叶斯算法(Naive Bayesian) 贝叶斯公式 \[P(A\mid B) = \frac{P(B\mid A)P(A)}{P(B)}\] 我们把P(A)称为"先 ...
- [ML学习笔记] 决策树与随机森林(Decision Tree&Random Forest)
[ML学习笔记] 决策树与随机森林(Decision Tree&Random Forest) 决策树 决策树算法以树状结构表示数据分类的结果.每个决策点实现一个具有离散输出的测试函数,记为分支 ...
- 学习笔记之Data analysis
Data analysis - Wikipedia https://en.wikipedia.org/wiki/Data_analysis Data analysis is a process of ...
- ML学习笔记之TF-IDF原理及使用
0x00 什么是TF-IDF TF-IDF(Term Frequency-Inverse Document Frequency, 词频-逆文件频率). # 是一种用于资讯检索与资讯探勘的常用加权技术. ...
- ML学习笔记- 神经网络
神经网络 有的模型可以有多种算法.而有的算法可能可用于多种模型.在神经网络中,对外部环境提供的模式样本进行学习训练,并能存储这种模式,则称为感知器;对外部环境有适应能力,能自动提取外部环境变化特征,则 ...
- ML学习笔记(1)
2019/03/09 16:16 归一化方法: 简单放缩(线性归一化):这种归一化方法比较适用在数值比较集中的情况.这种方法有个缺陷,如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用 ...
- ML学习笔记之LATEX数学公式基本语法
作者:@houkai本文为作者原创,转载请注明出处:https://www.cnblogs.com/houkai/p/3399646.html 0x00 概述 TEX 是Donald E. Knuth ...
随机推荐
- Spring事务传播属性介绍(三).Nested
Required.Required_New传播属性分析传送门:https://www.cnblogs.com/lvbinbin2yujie/p/10259897.html Mandatory.Neve ...
- webpack4 自学笔记五(tree-shaking)
全部的代码及笔记都可以在我的github上查看, 欢迎star: https://github.com/Jasonwang911/webpackStudyInit/tree/master/ThreeS ...
- Cannot find module 'socket.io'
That's all. Then I try to use socket.io with this line: var io = require('socket.io').listen(app); A ...
- 微信小程序开源Demo精选
来自:http://www.jianshu.com/p/0ecf5aba79e1 文/weapphome(简书作者)原文链接:http://www.jianshu.com/p/0ecf5aba79e1 ...
- Java基础——String类(一)
一.String 类代表字符串 Java 程序中的所有字符串字面值(如 "abc" )都作为此类的实例实现. 字符串是常量:它们的值在创建之后不能更改.字符串缓冲区支持可变的字符串 ...
- 在 CentOS7 上安装 RabbitMQ 消息队列中间件
RabbitMQ 是流行的开源消息队列系统,是 AMQP(Advanced Message Queuing Protocol 高级消息队列协议)的标准实现,用 erlang 语言开发.RabbitMQ ...
- java设计模式-----23、命令模式
概念: Command模式也叫命令模式 ,是行为设计模式的一种.Command模式通过被称为Command的类封装了对目标对象的调用行为以及调用参数. 命令模式(Command Pattern)是一种 ...
- python变量作用域,函数与传参
一.元组传值: 一般情况下函数传递参数是1对1,这里x,y是2个参数,按道理要传2个参数,如果直接传递元祖,其实是传递一个参数 >>> def show( x, y ): ... p ...
- 大数据java基础day01
day01笔记 1.==操作符和equals方法 equals方法存在于Object类中,所有类的equals方法都继承于Object 2.String类的常用方法 ①.replace()替换字符串 ...
- Angular 6.X CLI(Angular.json) 属性详解
Angular CLI(Angular.json) 属性详解 简介 angular cli 是angular commond line interface的缩写,意为angular的命令行接口.在an ...
