HDU 4940 Destroy Transportation system(无源汇上下界网络流)

Problem Description

Tom is a commander, his task is destroying his enemy’s transportation system.

Let’s represent his enemy’s transportation system as a simple
directed graph G with n nodes and m edges. Each node is a city and each
directed edge is a directed road. Each edge from node u to node v is
associated with two values D and B, D is the cost to destroy/remove such
edge, B is the cost to build an undirected edge between u and v.

His enemy can deliver supplies from city u to city v if and only if
there is a directed path from u to v. At first they can deliver supplies
from any city to any other cities. So the graph is a strongly-connected
graph.

He will choose a non-empty proper subset of cities,
let’s denote this set as S. Let’s denote the complement set of S as T.
He will command his soldiers to destroy all the edges (u, v) that u
belongs to set S and v belongs to set T.

To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:

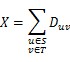
After that, all the edges from S to T are destroyed. In order to
deliver huge number of supplies from S to T, his enemy will change all
the remained directed edges (u, v) that u belongs to set T and v belongs
to set S into undirected edges. (Surely, those edges exist because the
original graph is strongly-connected)

To change an edge, they
must remove the original directed edge at first, whose cost is D, then
they have to build a new undirected edge, whose cost is B. The total
cost they will pay is Y. You can use this formula to calculate Y:

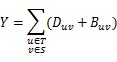
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy
that he is unwilling to take a cup of time to choose a set S to make
Y>=X, he hope to choose set S randomly! So he asks you if there is a
set S, such that Y<X. If such set exists, he will feel unhappy,
because he must choose set S carefully, otherwise he will become very
happy.

 

Input

There are multiply test cases.

The first line contains an integer T(T<=200), indicates the number of cases.

For each test case, the first line has two numbers n and m.

Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)

The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.

 

Output

For each case, output "Case #X: " first, X is the case number
starting from 1.If such set doesn’t exist, print “happy”, else print
“unhappy”.

 

Sample Input

2

3 3

1 2 2 2

2 3 2 2

3 1 2 2

3 3

1 2 10 2

2 3 2 2

3 1 2 2

 

Sample Output

Case #1: happy

Case #2: unhappy

 

Sample Output

In first sample, for any set S, X=2, Y=4.

In second sample. S= {1}, T= {2, 3}, X=10, Y=4.

题意

给你N个点M条边强连通的有向简单图，D代表删掉这个边的花费，D+B代表重建为双向边的花费，让你选择一个集合S，其余的点在T集合，X为u在S集合v在T集合的所有边的D之和，Y为u在T集合v在S集合的所有边的D+B之和，求是否存在一个集合S，使得X>Y，若存在输出unhappy，否则输出happy

题解

无源汇上下界网络流，下界D，上界D+B，判断是否存在可行流

若存在，则说明对于任意集合S，流出的流量=流入的流量，X<=流出的流量<=Y

建图每条边建为自由流（u，v，B）

对于每个点，设M为总流入-总流出

若M>0，则建（S，i，M）说明i需要多流出M

若M<0，则建（i，T，M）说明i需要多流入M

最后判断与S连的边是否全满流

代码

 #include<bits/stdc++.h>
 using namespace std;

 const int maxn=1e5+;
 const int maxm=2e5+;
 const int INF=0x3f3f3f3f;

 int TO[maxm],CAP[maxm],NEXT[maxm],tote;
 int FIR[maxn],gap[maxn],cur[maxn],d[maxn],q[];
 int n,m,S,T;

 void add(int u,int v,int cap)
 {
     TO[tote]=v;
     CAP[tote]=cap;
     NEXT[tote]=FIR[u];
     FIR[u]=tote++;

     TO[tote]=u;
     CAP[tote]=;
     NEXT[tote]=FIR[v];
     FIR[v]=tote++;
 }
 void bfs()
 {
     memset(gap,,sizeof gap);
     memset(d,,sizeof d);
     ++gap[d[T]=];
     for(int i=;i<=n;++i)cur[i]=FIR[i];
     int head=,tail=;
     q[]=T;
     while(head<=tail)
     {
         int u=q[head++];
         for(int v=FIR[u];v!=-;v=NEXT[v])
             if(!d[TO[v]])
                 ++gap[d[TO[v]]=d[u]+],q[++tail]=TO[v];
     }
 }
 int dfs(int u,int fl)
 {
     if(u==T)return fl;
     int flow=;
     for(int &v=cur[u];v!=-;v=NEXT[v])
         if(CAP[v]&&d[u]==d[TO[v]]+)
         {
             int Min=dfs(TO[v],min(fl,CAP[v]));
             flow+=Min,fl-=Min,CAP[v]-=Min,CAP[v^]+=Min;
             if(!fl)return flow;
         }
     if(!(--gap[d[u]]))d[S]=n+;
     ++gap[++d[u]],cur[u]=FIR[u];
     return flow;
 }
 int ISAP()
 {
     bfs();
     int ret=;
     while(d[S]<=n)ret+=dfs(S,INF);
     return ret;
 }
 void init()
 {
     tote=;
     memset(FIR,-,sizeof FIR);
 }
 int in[maxn];
 int main()
 {
     int t;
     scanf("%d",&t);
     for(int ca=;ca<=t;ca++)
     {
         init();
         memset(in,,sizeof in);
         scanf("%d%d",&n,&m);
         for(int i=,u,v,d,b;i<m;i++)
         {
             scanf("%d%d%d%d",&u,&v,&d,&b);
             add(u,v,b);
             in[u]-=d;
             in[v]+=d;
         }
         S=n+,T=S+,n+=;
         int sum=;
         for(int i=;i<=n;i++)
             if(in[i]>)
             {
                 add(S,i,in[i]);
                 sum+=in[i];
             }
             else if(in[i]<)
                 add(i,T,-in[i]);
         printf("Case #%d: %s\n",ca,ISAP()==sum?"happy":"unhappy");
     }
     return ;
 }