MT【85】正整数系数
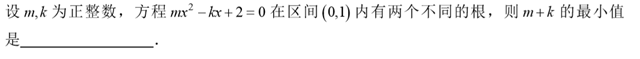
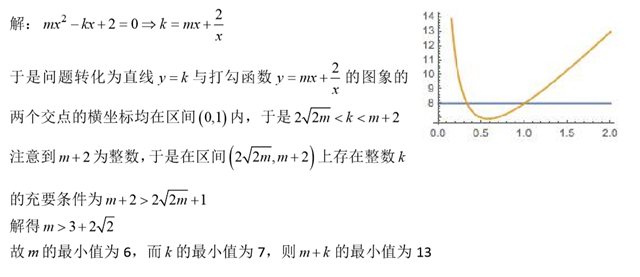
评:这类与正整数有关的题,是很多学生所不习惯以及无从下手的。事实上很多时候要用到整数的这个性质:$m>n,m,n\in Z$则$m\ge n+1$,这道题用二次函数区间上有根的一般做法也可以,大致是这样:

MT【85】正整数系数的更多相关文章
- Leaflet+heatmap实现离线地图加载和热力图应用
本人博客主页:http://www.cnblogs.com/webbest/ 2017年春节已经过完,新一年的奋斗也刚刚开始.今年要经历的挑战也是大大的...不扯了. 年底前软件项目相对较多,恰巧在年 ...
- MT【232】展开式中的系数
$(1+x+x^2+\cdots+x^{100})^3$展开式中$x^{150}$前的系数为_____ 解答:$(1+x+x^2+\cdots+x^{100})^3=(1-x^{101})^3\sum ...
- MT【224】反解系数
(2011安徽省赛)$f(x)=ax^3+bx+c(a,b,c\in R),$当$0\le x \le 1$时,$0\le f(x)\le 1$,求$b$的可能的最大值. 提示:取三个点$f(0),f ...
- MT【182】系数奇怪的二次函数
设函数$f(x)=3ax^2-2(a+b)x+b,$其中$a>0,b\in R$证明:当$0\le x\le 1$时,$|f(x)|\le \max\{f(0),f(1)\}$ 分析:由$a&g ...
- MT【95】由参数前系数凑配系数题2
提示:都是看$a,b$前的系数做的$a=4/3,b=2/3;a+b=\le2$,一样的可以求得$a+b$的最小值-1,当$b=\frac{1}{3},a=\frac{-4}{3}$时取到等号.此题是清 ...
- MT【94】由参数前系数凑配系数题1
评:根据$b,c$前系数凑配系数,也是比较常见的思路.
- MT【329】二次函数系数的最大最小
已知二次函数$f(x)=ax^2+bx+c$有零点,且$a+b+c=1$ 若$t=\min\{a,b,c\}$求$t$的最大值. 分析:由$a,c$的对称性,不妨$c\ge a$即$2a+b\le1$ ...
- MT【34】正余弦的正整数幂次快速表示成正余弦的线性组合
问题:如何快速把$cos^4xsin^3x$表示成正弦,余弦的线性组合? 分析:利用牛顿二项式展开以下表达式: 再利用欧拉公式$e^{i\theta}=cos\theta+isin\theta$ 比如 ...
- MT【37】二次函数与整系数有关的题
解析: 评:两根式是不错的考虑方向,一方面二次函数两根式之前有相应的经验,另一方面这里$\sqrt{\frac{b^2}{4}-c}$正好和两个根有关系.
随机推荐
- Jquery属性练习
<!DOCTYPE html> <html lang="en" xmlns="http://www.w3.org/1999/xhtml"> ...
- bash 定时任务
time1=$(date +%s -d '2014-01-13 22:46:05') for((;;)) do time2=$(date +%s) time3=$((time1 - time2)) ] ...
- 【chrome】"您的连接不是私密连接" 解决办法
1.启用显示证书选项 在Chrome的地址栏中输入:chrome://flags/#show-cert-link,选择"启用",重启Chrome浏览器. (操作过无用) 2.安装 ...
- Python+Matplotlib制作动画
注: 在"实验设计与数据处理"的课后作业中,有一个数据可视化的作业,利用课程上学习的某种方法找一个二维函数的最大值,并将这个寻找的过程可视化.在作业里面利用了Matplotlib的 ...
- 内幕:XX二手车直卖网,狗屁直卖网,我来揭开他们套路!
转自:明锐论坛 我是一位花生二手车直卖网的离职员工.已离职了一段时间,现在在某家汽车4S店公司上班.过去了那么久,每当看到他们铺天盖地的广告,心里都像十五个水桶--七上八下.思索已久,我还是决定鼓 ...
- Airmon-ng抓包&破解wifi
安装 aircrack获取(aircrack源) sudo apt-get install aircrack-ng 配置 安装组件 sudo apt-get install build-essent ...
- Teaching Machines to Understand Us 让机器理解我们 之二 深度学习的历史
Deep history 深度学习的历史 The roots of deep learning reach back further than LeCun’s time at Bell Labs. H ...
- 区块链--Bitcoin共识机制
目录 中心化和去中心化 比特币共识机制 拜占庭将军共识机制 比特币成功解决了拜占庭问题 中心化和去中心化 中心化模式: 优点:效率高 缺点:中间层次太多(组织层次连接) 去中心化模式: 缺点:效率低 ...
- 绕过用编码方式阻止XSS攻击的几个例子
阻止攻击的常用方法是:在将HTML返回给Web浏览器之前,对攻击者输入的HTML进行编码.HTML编码使用一些没有特定HTML意义的字符来代替那些标记字符(如尖括号).这些替代字符不会影响文本在web ...
- Linux内核的启动过程分析
秦鼎涛 <Linux内核分析>MOOC课程http://mooc.study.163.com/course/USTC-1000029000 一.实验目的及要求: 使用gdb跟踪调试内核从s ...
