带精英策略的快速非支配排序遗传算法 NSGA-II 算法

NSGAII（带精英策略的非支配排序的遗传算法），是基于遗传算法的多目标优化算法，是基于pareto最优解讨论的多目标优化，下面介绍pareto（帕累托）最优解的相关概念。

Paerot支配关系

Pareto最优解定义

多目标优化问题与单目标优化问题有很大差异。当只有一个目标函数时,人们寻找最好的解,这个解优于其他所有解,通常是全局最大或最小,即全局最优解。而当存在多个目标时,由于目标之间存在冲突无法比较,所以很难找到一个解使得所有的目标函数同时最优,也就是说,一个解可能对于某个目标函数是最好的,但对于其他的目标函数却不是最好的,甚至是最差的。因此,对于多目标优化问题,通常存在一个解集,这些解之间就全体目标函数而言是无法比较优劣的,其特点是:无法在改进任何目标函数的同时不削弱至少一个其他目标函数。这种解称作非支配解(nondominated soluitons)或Pareto最优解(Pareto optimal Soluitons),定义如下：

NSGAII算法

NSGA一II算法的基本思想为:首先,随机产生规模为N的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群;其次,从第二代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;最后,通过遗传算法的基本操作产生新的子代种群:依此类推,直到满足程序结束的条件。相应的程序流程图如下图所示：

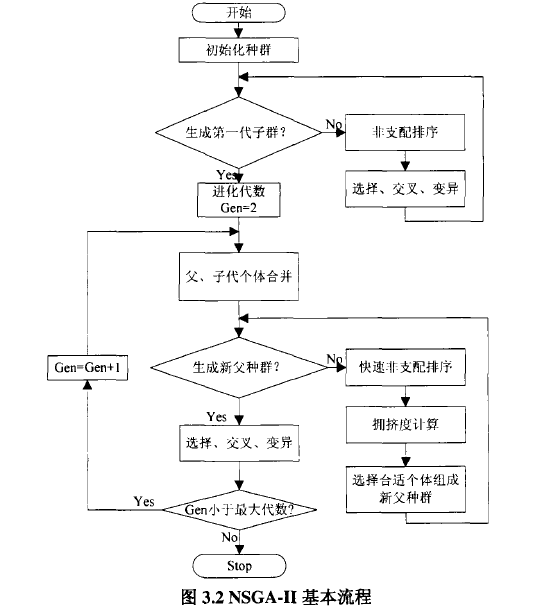
快速非支配排序算法

拥挤度和拥挤度比较算子

拥挤度是指种群中给定个体的周围个体的密度,直观上可表示为个体。周围仅仅包含个体。本身的最大长方形的长、宽之和， 用nd表示。

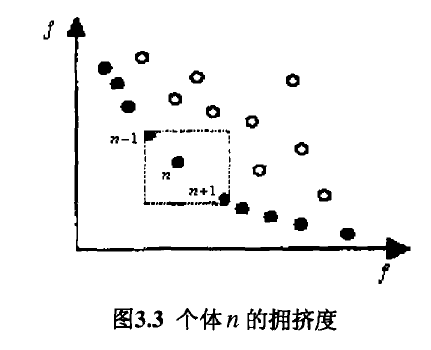
拥挤度的算法如下：

这里面有些小问题， 拥挤度无穷的设定并不是边界的两端而是一端， 如果是最小问题的话则是最小一端。

其中， 个体的拥挤距离  nd  最终是要除以该层 个体 在该目标函数上的范围（该层个体在该目标函数值上的最大最小值之差）

拥挤度比较算子

非支配排序遗传算法(NSGA)在许多问题上得到了应用,但NSGA仍存在一些问题:
)a计算复杂度较高,为O(mN3)(m为目标函数个数,N为种群大小),所以当种群较大时,计算相当耗时。
b)没有精英策略;精英策略可以加速算法的执行速度,而且也能在一定程度上确保己经找到的满意解不被丢失。
)c需要指定共享半径。

而NSGA一II针对以上的缺陷通过以下三个方面进行了改进:

)a提出了快速非支配排序法,降低了算法的计算复杂度。由原来的O(mN3)降到O(mN2),其中,m为目标函数个数,N为种群大小。
b)提出了拥挤度和拥挤度比较算子,代替了需要指定共享半径的适应度共享策略,并在快速排序后的同级比较中作为胜出标准,使准Paroet域中的个体能扩展到整个Pareto域,并均匀分布,保持了种群的多样性。
)c引入精英策略,扩大采样空间。将父代种群与其产生的子代种群组合,共同竞争产生下一代种群,有利于保持父代中的优良个体进入下一代,并通过对种群中所有个体的分层存放,使得最佳个体不会丢失,迅速提高种群水平。

主体循环部分

(1).随机初始化开始种群P₀。并对P₀进行非支配排序，初始化每个个体的rank值。

(2). t = 0

(3).通过二进制锦标赛法从P_t选择个体，并进行交叉和变异操作，产生新一代种群Q_t。

(4).通过合并P_t 和 Q_t 产生出组合种群R_t =  P_t UQ_t 。

(5).对R_t进行非支配排序，并通过排挤和精英保留策略选出N个个体，组成新一代种群P_t+1。

(6).跳转到步骤3，并循环，直至满足结束条件。

以上内容是结合以下网络上的资料给出的：

http://www.cnblogs.com/bnuvincent/p/5289710.html

https://www.zhihu.com/question/26990498

另外，继续学习推荐参考以下内容：

http://blog.csdn.net/lf8289/article/details/2291466