numpy和tensorflow中的广播机制

广播的引出

numpy两个数组的相加、相减以及相乘都是对应元素之间的操作。

import numpy as np

x = np.array([[2,2,3],[1,2,3]])
y = np.array([[1,1,3],[2,2,4]])
print(x*y)  #numpy当中的数组相乘是对应元素的乘积，与线性代数当中的矩阵相乘不一样
 
输入结果如下：
‘‘‘
[[ 2  2  9]
 [ 2  4 12]]
‘‘‘

当两个数组的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）。

比如，一个二维数组减去列平均值，来对数组的每一列进行距平化处理：

import numpy as np

arr = np.random.randn(4,3)  #shape(4,3)
arr_mean = arr.mean(0)      #shape(3,)
demeaned = arr -arr_mean

很明显上式arr和arr_mean维度并不形同，但是它们可以进行相减操作，这就是通过广播机制来实现的。

广播的原则

如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。

这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

数组维度不同，后缘维度的轴长相符

我们来看一个例子：

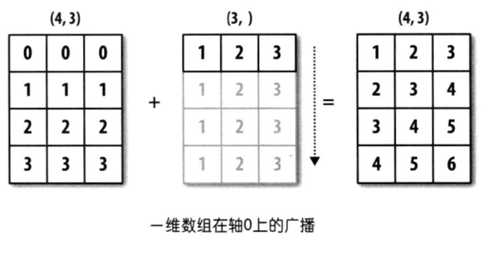
import numpy as np
 
arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])  #arr1.shape = (4,3)
arr2 = np.array([1, 2, 3])    #arr2.shape = (3,)
arr_sum = arr1 + arr2
print(arr_sum)
 
输入结果如下:
‘‘‘
[[1 2 3]
 [2 3 4]
[3 4 5]
[4 5 6]]
‘‘‘

上例中arr1的shape为（4,3），arr2的shape为（3，）。可以说前者是二维的，而后者是一维的。但是它们的后缘维度相等，arr1的第二维长度为3，和arr2的维度相同。arr1和arr2的shape并不一样，但是它们可以执行相加操作，这就是通过广播完成的，在这个例子当中是将arr2沿着0轴进行扩展。

上面程序当中的广播如下图所示：

同样的例子还有：

从上面的图可以看到，（3,4,2）和（4,2）的维度是不相同的，前者为3维，后者为2维。但是它们后缘维度的轴长相同，都为（4,2），所以可以沿着0轴进行广播。

同样，还有一些例子：（4,2,3）和（2,3）是兼容的，（4,2,3）还和（3）是兼容的，后者需要在两个轴上面进行扩展。

数组维度相同，其中有个轴为1

我们来看下面的例子：

import numpy as np
 
arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])  #arr1.shape = (4,3)
arr2 = np.array([[1],[2],[3],[4]])    #arr2.shape = (4, 1)
 
arr_sum = arr1 + arr2
print(arr_sum)
 
输出结果如下：
[[1 1 1]
 [3 3 3]
 [5 5 5]
 [7 7 7]]

arr1的shape为（4,3），arr2的shape为（4,1），它们都是二维的，但是第二个数组在1轴上的长度为1，所以，可以在1轴上面进行广播，如下图所示：

在这种情况下，两个数组的维度要保证相等，其中有一个轴的长度为1，这样就会沿着长度为1的轴进行扩展。这样的例子还有：（4,6）和（1,6）。（3,5,6）和（1,5,6）、（3,1,6）、（3,5,1），后面三个分别会沿着0轴，1轴，2轴进行广播。

后话：还有上面两种结合的情况，如（3,5,6）和（1,6）是可以相加的。在TensorFlow当中计算张量的时候也是用广播机制，并且和numpy的广播机制是一样的。