Gym 101981G - Pyramid - [打表找规律][2018-2019 ACM-ICPC Asia Nanjing Regional Contest Problem G]

题目链接：http://codeforces.com/gym/101981/attachments

The use of the triangle in the New Age practices seems to be very important as it represents the unholy
trinity (Satan, the Antichrist and the False Prophet bringing mankind to the New World Order with
false/distorted beliefs). The triangle is of primary importance in all Illuminati realms, whether in the
ritual ceremonies of the Rosicrucians and Masons or the witchcraft, astrological and black magic practices
of other Illuminati followers.
One day you found a class of mysterious patterns. The patterns can be classified into different degrees. A
pattern of degree n consists of n*(n+1)/2 small regular triangles with side length 1, all in the same direction,
forming a big triangle. The figure below shows the pattern of degree 3. All small regular triangles are
highlighted.

Since the pattern contains many regular triangles, which is very evil and unacceptable, you want to
calculate the number of regular triangles formed by vertices in the pattern, so that you can estimate the
strength of Illuminati. It is not necessary that each side of regular triangles is parallel to one side of the
triangles. The figure below shows two regular triangles formed by vertices in a pattern of degree 3.

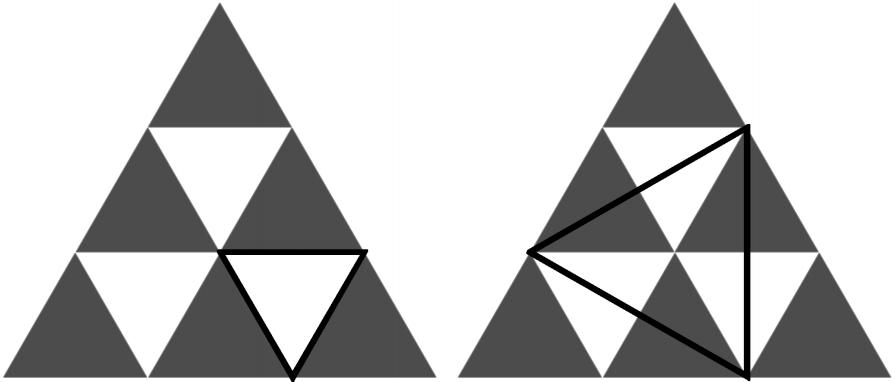
Since the answer can be very large, you only need to calculate the number modulo 10^9 + 7.

Input
The first line contains an integer t (1 ≤ t ≤ 10^6) — the number of test cases.
Each of the next t lines contains an integer n (1 ≤ n ≤ 10^9) — the degree of the pattern.

Output
For each test case, print an integer in one line — the number of regular triangles modulo 10^9 + 7.

Example
standard input
3

1

2

3

standard output
1

5

15

题意：

上面那个图形的度数为 $3$，里面包含了 $15$ 个正三角形。现在给出度数 $n$，让你找出那样一个图形里面包含多少个正三角形。

题解：

暴力打出度数在 $1 \sim 20$ 内的表，发现规律是三阶差分是等差数列 $4,5,6,7,\cdots$（真的我没有开玩笑……），或者说四阶差分是常数 $1$。然后果断推了个递推式用矩阵快速幂交了一发……TLE+1。

然后知道了只能 $O(1)$ 地求，开始考虑推通项公式。类比于四次函数求四阶导数之后为常数，换句话说通向公式应当是一个四次多项式。

因此可以假设 $a_n = An^4 + Bn^3 + Cn^2 + Dn + E$，然后将前五项 $a_1 = 1, a_2 = 5, a_3 = 15, a_4 = 35, a_5 = 70$ 代入解五元一次线性方程组，

解得 $A = \frac{1}{24}, B = \frac{1}{4}, C = \frac{11}{24}, D = \frac{1}{4}, E = 0$。

（注意不要忘了除法是乘逆元……已经有两次因为这个WA+n了……）

然后实际上，OEIS搜一下就可以知道 $a_n = C_{n+3}^{4}$。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+;
ll n;
ll fpow(ll a,ll n)
{
    ll res=,base=a%mod;
    while(n)
    {
        if(n&) res*=base, res%=mod;
        base*=base, base%=mod;
        n>>=;
    }
    return res%mod;
}
ll inv(ll a){return fpow(a,mod-);}
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%I64d",&n);
        ll ans=;
        ans+=fpow(n,), ans%=mod;
        ans+=*fpow(n,)%mod, ans%=mod;
        ans+=*fpow(n,)%mod, ans%=mod;
        ans+=*n%mod, ans%=mod;
        ans*=inv(), ans%=mod;
        printf("%I64d\n",ans);
    }
}