[LTR] 信息检索评价指标(RP/MAP/DCG/NDCG/RR/ERR)
一、RP
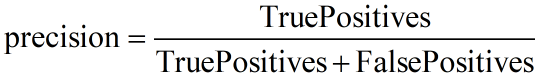
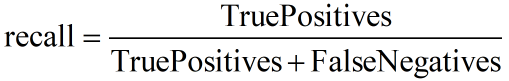
和 precision
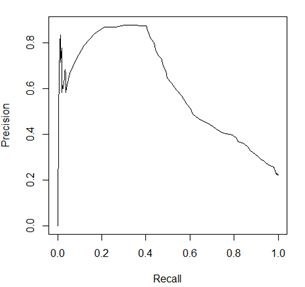
反映了模型性能的两个方面,单一依靠某个指标并不能较为全面的评价一个模型的性能。
recall 和 precision 的影响,较为全面的评价一个模型。
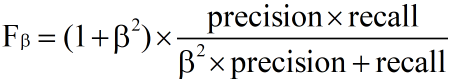
表示召回率比准确率重要一倍;F0.5-Score 表示准确率比召回率重要一倍。
二、MAP
Precision),即
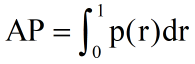
的计算是对排序位置敏感的,相关文档排序的位置越靠前,检索出相关的文档越多,AP 值越大。
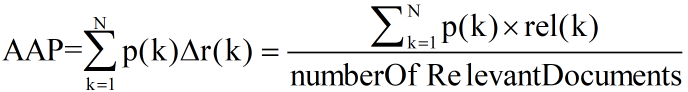
其中,N 代表所有相关文档的总数,p(k) 表示能检索出 k 个相关文档时的 precision 值,而
△r(k) 则表示检索相关文档个数从 k-1 变化到 k 时(通过调整阈值)recall 值的变化情况。
个文档是否相关,若相关则为1,否则为0,则可以简化公式为:
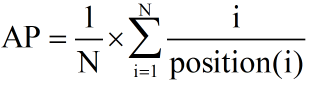
表示相关文档总数,position(i) 表示第 i 个相关文档在检索结果列表中的位置。
Precision)即多个查询的平均正确率(AP)的均值,从整体上反映模型的检索性能。
对应总共有5个相关文档。当通过模型执行查询1、2时,分别检索出4个相关文档(Rank=1、2、4、7)和3个相关文档(Rank=1、3、5)。
MAP=(0.83+0.45)/2=0.64。
三、NDCG
1、CG(Cumulative Gain)累计效益
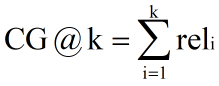
k 表示 k 个文档组成的集合,rel 表示第 i 个文档的相关度,例如相关度分为以下几个等级:
| Relevance Rating | Value |
| Perfect | 5 |
| Excellent | 4 |
| Good | 3 |
| Fair | 2 |
| Simple | 1 |
| Bad | 0 |
2、DCG(Discounted Cumulative Gain)
CG 的计算公式得出的排名是相同的,但是显然前者的排序好一些。
1/log2(i+1),其中
log2(i+1)
为折扣因子;
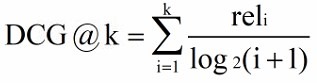
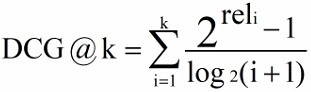
3、IDCG(ideal DCG)
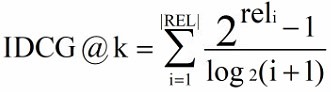
4、NDCG(Normalized
DCG)
的计算结果。所以不能简单的对不同查询的 DCG 结果进行平均,需要先归一化处理。
相差多大:
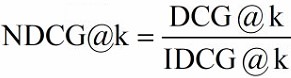
NDCG。
5、例子
List,当假设用户的选择与排序结果无关,则根据相关度生成的累计增益如下图所示:
| URL | rel | Gain(2reli-1) | Cumulative Gain | |
| #1 | http://abc.go.com | 5 | 31 | 31 |
| #2 | http://www.abctech.com | 2 | 3 | 34=31+3 |
| #3 | http://abcnews.go.com/sections/ | 4 | 15 | 49=31+3+15 |
| #4 | http://www.abc.net.au/ | 4 | 15 | 64=31+3+15+15 |
| #5 | http://abcnews.com/ | 4 | 15 | 79=31+3+15+15+15 |
| #6 | ... | ... | ... | ... |
factor):1/(log(i+1)/log2) = log2/log(i+1)。
| URL | rel | Gain(2reli-1) | Cumulative Gain |
DCG | |
| #1 | http://abc.go.com | 5 | 31 | 31 | 31=31×1 |
| #2 | http://www.abctech.com | 2 | 3 | 34=31+3 | 32.9=31+3×0.63 |
| #3 | http://abcnews.go.com/sections/ | 4 | 15 | 49=31+3+15 | 40.4=32.9+15×0.50 |
| #4 | http://www.abc.net.au/ | 4 | 15 | 64=31+3+15+15 | 46.9=40.4+15×0.43 |
| #5 | http://abcnews.com/ | 4 | 15 | 79=31+3+15+15+15 | 52.7=46.9+15×0.39 |
| #6 | ... | ... | ... | ... | ... |
而理想的情况,根据相关度 rel 递减排序后计算 DCG:
| URL | rel | Gain(2reli-1) | IDCG(Max DCG) |
|
| #1 | http://abc.go.com | 5 | 31 | 31=31×1 |
| #3 | http://abcnews.go.com/sections/ | 4 | 15 | 40.5=31+15×0.63 |
| #4 | http://www.abc.net.au/ | 4 | 15 | 48.0=40.5+15×0.5 |
| #5 | http://abcnews.com/ | 4 | 15 | 54.5=48.0+15×0.43 |
| #7 | http://abc.org/ | 4 | 15 | 60.4=54.5+15×0.39 |
| #9 | ... | ... | ... | ... |
所以最终得出 NDCG 结果:
| URL | rel | Gain(2reli-1) | Cumulative Gain |
DCG | IDCG(Max DCG) | NDCG | |
| #1 | http://abc.go.com | 5 | 31 | 31 | 31=31×1 | 31=31×1 | 1=31/31 |
| #2 | http://www.abctech.com | 2 | 3 | 34=31+3 | 32.9=31+3×0.63 | 40.5=31+15×0.63 | 0.81=32.9/40.5 |
| #3 | http://abcnews.go.com/sections/ | 4 | 15 | 49=31+3+15 | 40.4=32.9+15×0.50 | 48.0=40.5+15×0.5 | 0.84=40.4/48.0 |
| #4 | http://www.abc.net.au/ | 4 | 15 | 64=31+3+15+15 | 46.9=40.4+15×0.43 | 54.5=48.0+15×0.43 | 0.86=46.9/54.5 |
| #5 | http://abcnews.com/ | 4 | 15 | 79=31+3+15+15+15 | 52.7=46.9+15×0.39 | 60.4=54.5+15×0.39 | 0.87=52.7/60.4 |
| #6 | ... | ... | ... | ... | ... | ... |
四、ERR
1、RR(reciprocal rank)
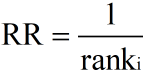
2、MRR(mean reciprocal
rank)
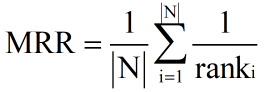
i 个查询的第一个相关文档的排名。
3、Cascade Model(瀑布模型)
i 个位置的文档项被点击的概率为:
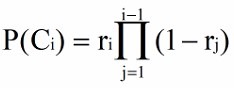
i 个文档被点击的概率,前 i-1 个文档则没有被点击,概率均为 1-rj;
4、ERR(Expected reciprocal rank)
计算第一个相关文档的位置倒数不同。
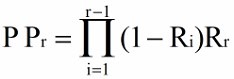
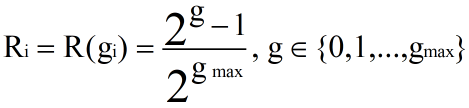
g 表示文档的相关度,参考 NDCG 中的 rel。
不一定是计算用户需求满足时停止的位置的倒数的期望,它可以是基于位置的函数 φ(r)
,只要满足 φ(0)=1,且随着 r→∞,φ(r)→0。
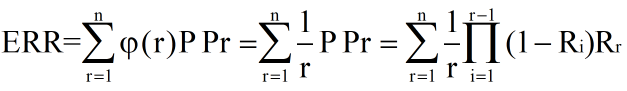
时就是 ERR,当 φ(r)=1/log2(r+1) 就是DCG。
参考链接:
[LTR] 信息检索评价指标(RP/MAP/DCG/NDCG/RR/ERR)的更多相关文章
- Kendall’s tau-b,pearson、spearman三种相关性的区别(有空整理信息检索评价指标)
同样可参考: http://blog.csdn.net/wsywl/article/details/5889419 http://wenku.baidu.com/link?url=pEBtVQFzTx ...
- [Scala] 实现 NDCG
一.关于 NDCG [LTR] 信息检索评价指标(RP/MAP/DCG/NDCG/RR/ERR) 二.代码实现 1.训练数据的加载解析 import scala.io.Source /* * 训练行数 ...
- Learning To Rank之LambdaMART前世今生
1. 前言 我们知道排序在非常多应用场景中属于一个非常核心的模块.最直接的应用就是搜索引擎.当用户提交一个query.搜索引擎会召回非常多文档,然后依据文档与query以及用户的相关程度对 ...
- [笔记]Learning to Rank算法介绍:RankNet,LambdaRank,LambdaMart
之前的博客:http://www.cnblogs.com/bentuwuying/p/6681943.html中简单介绍了Learning to Rank的基本原理,也讲到了Learning to R ...
- Learning to Rank算法介绍:RankNet,LambdaRank,LambdaMart
之前的博客:http://www.cnblogs.com/bentuwuying/p/6681943.html中简单介绍了Learning to Rank的基本原理,也讲到了Learning to R ...
- 推荐系统排序(Ranking)评价指标
一.准确率(Precision)和召回率(Recall) (令R(u)是根据用户在训练集上的行为给用户作出的推荐列表,而T(u)是用户在测试集上的行为列表.) 对用户u推荐N个物品(记为R(u) ...
- 百度Map调用
baiduMap API 根据地址查询经纬度 http://api.map.baidu.com/geocoder?address=要查询的地址&output=json&key=你的ke ...
- SPOJ - ADAFIELD ,Set+map,STL不会超时!
ADAFIELD - Ada and Field 这个题,如果用一个字来形容的话:-----------------------------------------------嗯! 题意:n*m的空白 ...
- go语言之进阶篇json解析到map
1.json解析到map(通过类型断言,找到值和value类型) 示例: package main import ( "encoding/json" "fmt" ...
随机推荐
- Flex中创建Accordion报错
1.错误描述 2.错误原因 <mx:Accordion width="100%" height="100%"> <s:NavigatorCon ...
- 前端框架Vue入门
1.Vue简介 Vue是一套构建用户界面的渐进性框架.Vue采用自底向上增量开发的设计,其关注点在图层,与angular的区别就在这里,它关注的是图层,而angular注释的是数据. 2.与React ...
- 对ajax回调函数的研究
1.1开发中遇到的问题 最近开发中我和同事都碰到这样的问题,我们使用jQuery的ajax方法做服务端的校验,在success方法里将验证结果存储到一个js的公共变量或者是页面里的隐藏域,接下来的代码 ...
- Shell 的特殊变量
2017-08-02 1.$0 获取当前脚本的名称或全路径 cat name.sh Linux shell sh name.sh echo $0 name.sh 2.$n(n >=1) 获取脚本 ...
- 【BZOJ3143】游走(高斯消元,数学期望)
[BZOJ3143]游走(高斯消元,数学期望) 题面 BZOJ 题解 首先,概率不会直接算... 所以来一个逼近法算概率 这样就可以求出每一条边的概率 随着走的步数的增多,答案越接近 (我卡到\(50 ...
- 【BZOJ1500】【NOI2005】维修数列(Splay)
[BZOJ1500][NOI2005]维修数列(Splay) 题面 不想再看见这种毒瘤题,自己去BZOJ看 题解 Splay良心模板题 真的很简单 我一言不发 #include<iostream ...
- [BZOJ3223] [Tyvj1729] 文艺平衡树 (splay)
Description 您需要写一种数据结构(可参考题目标题),来维护一个有序数列,其中需要提供以下操作:翻转一个区间,例如原有序序列是5 4 3 2 1,翻转区间是[2,4]的话,结果是5 2 3 ...
- 来谈谈JAVA面向对象 - 鲁班即将五杀,大乔送他回家??
开发IDE为Eclipse或者MyEclipse. 首先,如果我们使用面向过程的思维来解决这个问题,就是第一步做什么,第二步做什么? 鲁班即将五杀,大乔送他回家 这个现象可以简单地拆分为两步,代码大概 ...
- js如何开发游戏(聊天篇)
公司最近有这方面的需求,期望我们能搞出点有趣的小游戏来帮助公司进行推广,公司没有专门做游戏开发的员工,很不幸这件事情掉到了前端头上. 我记得我以前在学习的时候曾经见过一些厉害的前端工程师编写过一些网页 ...
- APNS IOS 消息推送处理失效的Token
在开发苹果推送服务时候,要合理的控制ios设备的Token,而这个Token是由苹果服务器Apns产生的,就是每次app问Apns要Token,由苹果服务器产生的Token会记录到Apns里面,我们需 ...
