c++实验9 图及图的操作实验
实验9 图及图的操作实验
--博客后半部分有程序的所有代码--
1、图邻接矩阵存储结构表示及基本操作算法实现
（1）邻接矩阵存储结构类定义：
#include "SeqList.h" //包含动态数组结构的顺序表类
#include "SeqQueue.h" //包含静态数组结构的顺序队列类
typedef char VerT; //定义邻接矩阵图类中的VerT class AdjMWGraph
{
private:
SeqList Vertices; //顶点顺序表
int Edge[MaxVertices][MaxVertices]; //边权值数组
double numOfEdges; //边的个数
void DepthFirstSearch(const int v, int visited[]);
void BroadFirstSearch(const int v, int visited[]);
public:
AdjMWGraph(const int sz=MaxVertices); //构造函数
~AdjMWGraph(void){}; //析构函数
int NumOfVertices(void) //取顶点个数
{return Vertices.Size();}
int NumOfEdges(void) //取边的个数
{return numOfEdges;}
Void Show(); //输出邻接矩阵结果
VerT GetValue(const int v); //取顶点数值
int GetWeight(const int v1, const int v2); //取边的权值
void InsertVertex(const VerT &vertex); //插入顶点
void InsertWayEdge(const int v1, const int v2, int weight);//插入边
void InsertNoWayEdge(const int v1, const int v2, int weight);//插入边
void DeleteVertex(const int v); //删除顶点
void DeleteEdge(const int v1, const int v2); //删除边
int GetFirstNeighbor(const int v); //取第一个邻接顶点
int GetNextNeighbor(const int v1, const int v2);//取下一个邻接顶点
void DepthFirstSearch(); //深度优先遍历
void BroadFirstSearch(); //广度优先遍历
};
struct RowColWeight //网的结构体
{ int row; //行下标
int col; //列下标
int weight; //权值
};
struct RowCol //图的结构体
{
int row; //行下标
int col; //列下标
};
（2）创建邻接矩阵算法
①创建无向图邻接矩阵算法：
void CreatNoWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向图参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, );
G.InsertNoWayEdge(E[k].col, E[k].row, );
}
}
②创建无向网邻接矩阵算法：
void CreatNoWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向网参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight);
G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight);
}
③创建有向图邻接矩阵算法：
void CreatWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e)
//在图G中插入n个顶点V 和 e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col,);
}
④创建有向网邻接矩阵算法：
void CreatWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e)
//在图G中插入n个顶点V 和 e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col, E[k].weight);
}
（3）输出邻接矩阵结果算法
int AdjMWGraph::Show()
{
for(int i=;i<Vertices.Size();i++)
{
for(int j=;j<Vertices.Size();j++)
{
int a=GetWeight(i,j);
if(a==MaxWeight)
cout<<"∞ ";
else
cout<<a<<" ";
}
cout<<endl;
}
}
测试数据：
int main()
{
AdjMWGraph g,f;
char a[] = {'A','B','C','D','E'};
char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{,,},{,,},{,,},{,,},{,,}};
RowColWeight r2[] ={{,,},{,,},{,,},{,,},{,,},{,,}};
int n1,n2,e1,e2;
n1=sizeof(a)/sizeof(a[]);
n2=sizeof(b)/sizeof(b[]);
e1=sizeof(r1)/sizeof(r1[]);
e2=sizeof(r2)/sizeof(r2[]);
CreatWayWeb(g, a, n1, r1, e1); //创建有向网
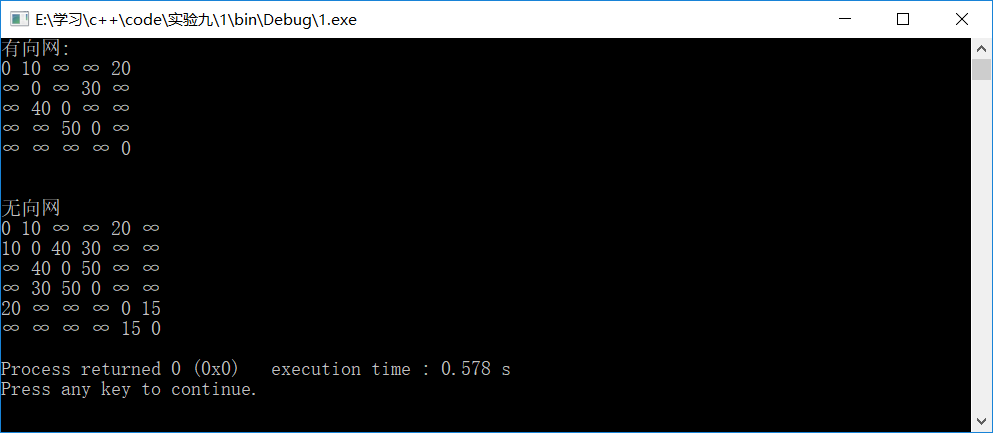
CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl;
g.Show(); cout<<"\n\n无向网"<<endl;
f.Show(); return ;
}
结果：
2、图的遍历递归算法
（1）（存储结构为邻接矩阵）深度优先遍历算法
void AdjMWGraph::DepthFirstSearch(const int v, int visited[])
//连通图G以v为初始顶点序号
//数组visited标记了相应顶点是否已访问过，
// 0表示未访问，1表示已访问
{
cout<<GetValue(v)<<" "; //访问该顶点
visited[v] = ; //置已访问标记
//取第一个邻接顶点
int w = GetFirstNeighbor(v);
//当邻接顶点存在时循环
while(w != -)
{
if(! visited[w])
DepthFirstSearch(w, visited); //递归
w = GetNextNeighbor(v, w); //取下一个邻接顶点
}
}
void AdjMWGraph::DepthFirstSearch()
{
int *visited = new int[NumOfVertices()];
//初始化访问标记
for(int i = ; i < NumOfVertices(); i++)
visited[i] = ;
//深度优先遍历
for(int i = ; i < NumOfVertices(); i++)
if(! visited[i])
DepthFirstSearch(i, visited);
delete []visited;
}
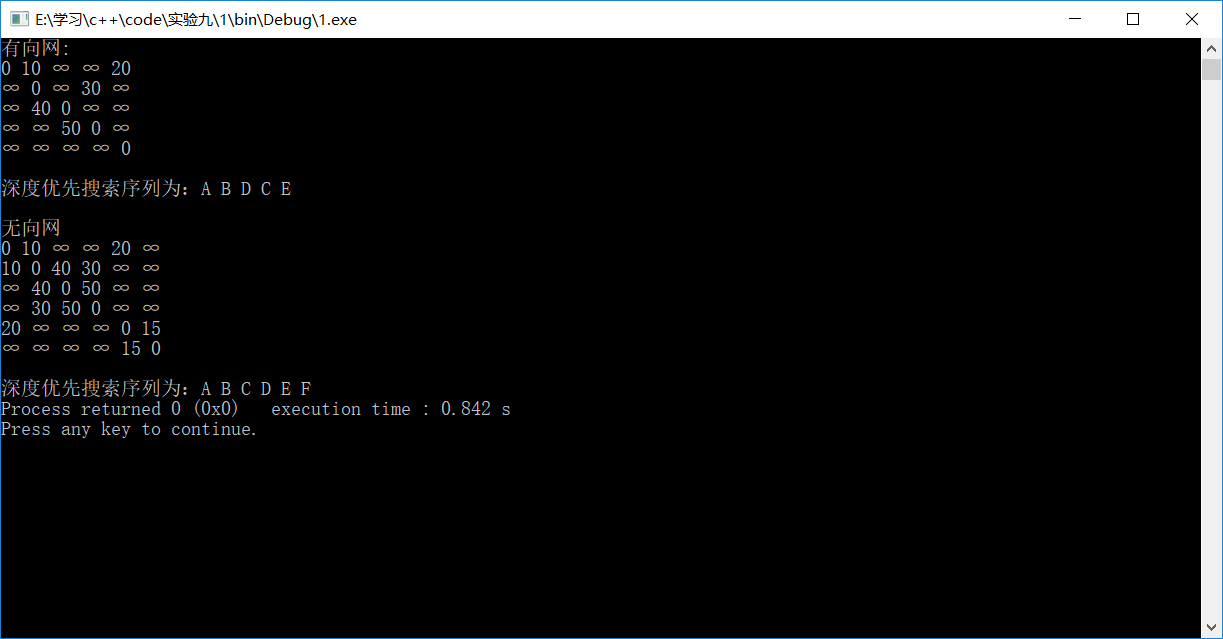
有向/无向网的测试结果：
（2）广度优先遍历算法
void AdjMWGraph::BroadFirstSearch(const int v, int visited[])
{
VerT u;
int w;
SeqQueue queue; //定义队列
cout<<GetValue(v)<<" "; //访问该顶点
visited[v] = ; //置已访问标记
queue.Append(v); //顶点v入队列
while(queue.NotEmpty()) //队列非空时循环
{
u = queue.Delete(); //出队列
w = GetFirstNeighbor(u); //取顶点u的第一个邻接顶点
while(w != -) //邻接顶点存在时
{
if(!visited[w]) //若该顶点没有访问过
{
cout<<GetValue(w)<<" "; //访问该顶点
visited[w] = ; //置已访问标记
queue.Append(w); //顶点w入队列
}
w = GetNextNeighbor(u, w);
}
}
} void AdjMWGraph::BroadFirstSearch()
//非连通图G访问操作为Visit()的广度优先遍历
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++)
visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(!visited[i])
BroadFirstSearch(i, visited);
delete []visited;
}
有向网/无向网的测试结果：
最后附上整体代码结构与结果
AdjMWGraph.h
#include "SeqList.h" //包含动态数组结构的顺序表类
#include "SeqQueue.h" //包含静态数组结构的顺序队列类
typedef char VerT; //定义邻接矩阵图类中的VerT class AdjMWGraph
{
private:
SeqList Vertices; //顶点顺序表
int Edge[MaxVertices][MaxVertices]; //边权值数组
double numOfEdges; //边的个数
void DepthFirstSearch(const int v, int visited[]);
void BroadFirstSearch(const int v, int visited[]);
public:
AdjMWGraph(const int sz=MaxVertices); //构造函数
~AdjMWGraph(void){}; //析构函数
void Show(); //输出邻接矩阵结果
int NumOfVertices(void) //取顶点个数
{return Vertices.Size();}
int NumOfEdges(void) //取边的个数
{return numOfEdges;}
VerT GetValue(const int v); //取顶点数值
int GetWeight(const int v1, const int v2); //取边的权值
void InsertVertex(const VerT &vertex); //插入顶点
void InsertWayEdge(const int v1, const int v2, int weight);//插入边
void InsertNoWayEdge(const int v1, const int v2, int weight);//插入边
void DeleteVertex(const int v); //删除顶点
void DeleteEdge(const int v1, const int v2); //删除边
int GetFirstNeighbor(const int v); //取第一个邻接顶点
int GetNextNeighbor(const int v1, const int v2);//取下一个邻接顶点
void DepthFirstSearch(); //深度优先遍历
void BroadFirstSearch(); //广度优先遍历
};
AdjMWGraph::AdjMWGraph(const int sz): Vertices(sz)
//构造函数 ,构造顶点个数为sz个，没有边的图
{
for(int i = ; i < sz; i++)
for(int j = ; j < sz; j++)
{
if(i == j)
Edge[i][j] = ;
else
Edge[i][j] = MaxWeight;
} // MaxWeight权值的无穷大
numOfEdges = ;
}
VerT AdjMWGraph::GetValue(const int v)
//取顶点v的数值
{
if(v < || v >= Vertices.Size())
{
cout << "参数v越界出错!" << endl;
exit();
}
return Vertices.GetData(v);
}
int AdjMWGraph::GetWeight(const int v1, const int v2)
//取起始顶点为v1、终止顶点为 v2的边的权值
{
if(v1 < || v1 >= Vertices.Size() || v2 < || v2 >= Vertices.Size())
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
return Edge[v1][v2];
} void AdjMWGraph::InsertVertex(const VerT &vertex)
//插入顶点vertex //把顶点vertex插入到顺序表的当前表尾位置
{ Vertices.Insert(vertex, Vertices.Size());
}
void AdjMWGraph::InsertWayEdge(const int v1, const int v2, int weight)
//插入一条起始顶点为v1、终止顶点为 v2、权值为weight的边
{
if(v1 < ||v1>=Vertices.Size()||v2 < ||v2 >=Vertices.Size())
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
Edge[v1][v2] = weight; //插入边
numOfEdges++; //边的个数加1
}void AdjMWGraph::InsertNoWayEdge(const int v1, const int v2, int weight)
//插入一条起始顶点为v1、终止顶点为 v2、权值为weight的边
{
if(v1 < ||v1>=Vertices.Size()||v2 < ||v2 >=Vertices.Size())
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
Edge[v1][v2] = weight; //插入边
numOfEdges+=0.5; //边的个数加0.5
}
void AdjMWGraph::DeleteVertex(const int v)
//删除顶点v
{
//删除所有包含顶点v的边
for(int i = ; i < Vertices.Size(); i++)
for(int j = ; j < Vertices.Size(); j++)
if((i == v || j == v) && i != j && Edge[i][j] > && Edge[i][j] < MaxWeight)
{
Edge[i][j] = MaxWeight; //把该边的权值置为无穷大
numOfEdges--; //边的个数减1
}
Vertices.Delete(v); //删除顶点v
}
void AdjMWGraph::DeleteEdge(const int v1, const int v2)
//删除一条起始顶点为v1、终止顶点为 v2的边
{
if(v1 < || v1 >Vertices.Size()||v2<||v2>Vertices.Size())
{
cout<<Vertices.Size();
cout << "参数v1或v2出错!" << endl;
exit();
}
if(Edge[v1][v2] == MaxWeight )
{
cout << "该边不存在!" << endl;
exit();
}
Edge[v1][v2] = MaxWeight; //把该边的权值置为无穷大
numOfEdges--; //边的个数减1
}
int AdjMWGraph::GetFirstNeighbor(const int v)
//取顶点v的第一个邻接顶点。若存在返回该顶点的下标序号，否则返回-1
{
if(v< || v> Vertices.Size())
{
cout << "参数v1越界出错!" << endl;
exit();
}
for(int col = ; col <=Vertices.Size(); col++)
if(Edge[v][col] > && Edge[v][col] < MaxWeight)
return col;
return -;
} int AdjMWGraph::GetNextNeighbor(const int v1, const int v2)
//取顶点v1的邻接顶点v2后的邻接顶点
//若存在返回该顶点的下标序号，否则返回-1
{
if(v1 < || v1 > Vertices.Size() || v2 < || v2 >Vertices.Size())
{
cout << "参数v1或v2越界出错!" << endl;
exit();
}
for(int col = v2+; col < Vertices.Size(); col++)
if(Edge[v1][col] > && Edge[v1][col] < MaxWeight)
return col;
return -;
}
void AdjMWGraph::DepthFirstSearch(const int v, int visited[])
//连通图G以v为初始顶点序号
//数组visited标记了相应顶点是否已访问过，
// 0表示未访问，1表示已访问
{
cout<<GetValue(v)<<" "; //访问该顶点
visited[v] = ; //置已访问标记
//取第一个邻接顶点
int w = GetFirstNeighbor(v);
//当邻接顶点存在时循环
while(w != -)
{
if(! visited[w])
DepthFirstSearch(w, visited); //递归
w = GetNextNeighbor(v, w); //取下一个邻接顶点
}
}
void AdjMWGraph::DepthFirstSearch()
{
int *visited = new int[NumOfVertices()];
//初始化访问标记
for(int i = ; i < NumOfVertices(); i++)
visited[i] = ;
//深度优先遍历
for(int i = ; i < NumOfVertices(); i++)
if(! visited[i])
DepthFirstSearch(i, visited);
delete []visited;
} void AdjMWGraph::BroadFirstSearch(const int v, int visited[])
{
VerT u;
int w;
SeqQueue queue; //定义队列
cout<<GetValue(v)<<" "; //访问该顶点
visited[v] = ; //置已访问标记
queue.Append(v); //顶点v入队列
while(queue.NotEmpty()) //队列非空时循环
{
u = queue.Delete(); //出队列
w = GetFirstNeighbor(u); //取顶点u的第一个邻接顶点
while(w != -) //邻接顶点存在时
{
if(!visited[w]) //若该顶点没有访问过
{
cout<<GetValue(w)<<" "; //访问该顶点
visited[w] = ; //置已访问标记
queue.Append(w); //顶点w入队列
}
w = GetNextNeighbor(u, w);
}
}
} void AdjMWGraph::BroadFirstSearch()
//非连通图G访问操作为Visit()的广度优先遍历
{
int *visited = new int[NumOfVertices()];
for(int i = ; i < NumOfVertices(); i++)
visited[i] = ;
for(int i = ; i < NumOfVertices(); i++)
if(!visited[i])
BroadFirstSearch(i, visited);
delete []visited;
}
void AdjMWGraph::Show()
{
for(int i=;i<Vertices.Size();i++)
{
for(int j=;j<Vertices.Size();j++)
{
int a=GetWeight(i,j);
if(a==MaxWeight)
cout<<"∞ ";
else
cout<<a<<" ";
}
cout<<endl;
}
}
CreatAdjMWGraph.h
struct RowColWeight //网的结构体
{ int row; //行下标
int col; //列下标
int weight; //权值
};
struct RowCol //图的结构体
{
int row; //行下标
int col; //列下标
}; void CreatWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e)
//在图G中插入n个顶点V 和 e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col, E[k].weight);
}
void CreatNoWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向网参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight);
G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight);
}
}
void CreatWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e)
//在图G中插入n个顶点V 和 e条边E
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
G.InsertWayEdge(E[k].row, E[k].col,);
}
void CreatNoWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e)
{
//在图G中插入n个顶点
for(int i = ; i < n; i++)
G.InsertVertex(V[i]);
//在图G中插入e条边
for(int k = ; k < e; k++)
{
if(E[k].row>E[k].col)
{
cout<<"无向图参数输入错误";
exit();
}
G.InsertNoWayEdge(E[k].row, E[k].col, );
G.InsertNoWayEdge(E[k].col, E[k].row, );
}
}
SeqList.h
class SeqList
{
protected:
DataType *list; //数组
int maxSize; //最大元素个数
int size; //当前元素个数
public:
SeqList(int max=); //构造函数
~SeqList(void); //析构函数 int Size(void) const; //取当前数据元素个数
void Insert(const DataType& item, int i);//插入
DataType Delete(const int i); //删除
DataType GetData(int i) const; //取数据元素
}; SeqList::SeqList(int max) //构造函数
{
maxSize = max;
size = ;
list = new DataType[maxSize];
} SeqList::~SeqList(void) //析构函数
{
delete []list;
} int SeqList::Size(void) const //取当前数据元素个数
{
return size;
} void SeqList::Insert(const DataType& item, int i) //插入
//在指定位置i前插入一个数据元素item
{
if (size == maxSize)
{
cout << "顺序表已满无法插入！" << endl;
exit();
}
if(i < || i > size) //参数正确与否判断
{
cout << "参数i越界出错!" << endl;
exit();
} //从size-1至i逐个元素后移
for(int j = size; j > i; j--) list[j] = list[j-]; list[i] = item; //在i位置插入item
size++; //当前元素个数加1
} DataType SeqList::Delete(const int i) //删除
//删除指定位置i的数据元素，删除的元素由函数返回
{
if (size == )
{
cout << "顺序表已空无元素可删！" << endl;
exit();
}
if(i < || i > size - ) //参数正确与否判断
{
cout<<"参数i越界出错!"<<endl;
exit();
} DataType x = list[i]; //取到要删除的元素 //从i+1至size-1逐个元素前移
for(int j = i;j < size-; j++) list[j] = list[j+]; size--; //当前元素个数减1
return x; //返回删除的元素
} DataType SeqList::GetData(int i) const //取数据元素
//取位置i的数据元素，取到的数据元素由函数返回
{
if(i < || i > size - ) //参数正确与否判断
{
cout << "参数i越界出错!" << endl;
exit();
} return list[i]; //返回取到的元素
}
SeqQueue.h
class SeqQueue{
private:
DataType data[]; //顺序队列数组
int front; //队头指示器
int rear; //队尾指示器
int count; //元素个数计数器
int maxsize;
public:
SeqQueue(); //构造函数
~SeqQueue(void){}; //析构函数
void Append(const DataType& item); //入队列
int NotEmpty(void)const //非空否
{return count!=;}
DataType Delete(void); //出队列
};
SeqQueue::SeqQueue()
{
front=rear=;
count=;
};
void SeqQueue::Append(const DataType& item) //入队列
//把数据元素item插入队列作为当前的新队尾
{
if(count>&&front==rear)
{
cout<<"队列已满!"<<endl;
exit();
}
data[rear]=item; //把元素item加在队尾
rear=(rear+) % maxsize; //队尾指示器加1
count++; //计数器加1
}
DataType SeqQueue::Delete(void) //出队列
//把队头元素出队列，出队列元素由函数返回
{
if(count==)
{
cout<<"队列已空!"<<endl;
exit();
}
DataType temp=data[front]; //保存原队头元素
front=(front+) % maxsize; //队头指示器加1
count--; //计数器减1
return temp; //返回原队头元素
}
main.cpp
#include <iostream>
#include <stdlib.h>
using namespace std;
typedef char VerT; //定义邻接矩阵图类中的VerT
typedef char DataType; //定义顺序表类中的DataType
const int MaxVertices = ; //定义最大顶点个数
const int MaxWeight = ; //定义权值的无穷大
#include "AdjMWGraph.h"//包含邻接矩阵的图类
#include "CreatAdjMWGraph.h"//包含邻接矩阵图的创建函数 int main()
{
AdjMWGraph g,f;
char a[] = {'A','B','C','D','E'};
char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{,,},{,,},{,,},{,,},{,,}};
RowColWeight r2[] ={{,,},{,,},{,,},{,,},{,,},{,,}};
int n1,n2,e1,e2;
n1=sizeof(a)/sizeof(a[]);
n2=sizeof(b)/sizeof(b[]);
e1=sizeof(r1)/sizeof(r1[]);
e2=sizeof(r2)/sizeof(r2[]);
CreatWayWeb(g, a, n1, r1, e1); //创建有向网
CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl;
g.Show();
cout << "\n顶点个数为：" << g.NumOfVertices();
cout << "\n边的条数为：" << g.NumOfEdges();
cout << "\n深度优先搜索序列为：";
g.DepthFirstSearch();
cout << "\n广度优先搜索序列为：";
g.BroadFirstSearch(); cout<<"\n\n无向网"<<endl;
f.Show();
cout << "\n顶点个数为：" << f.NumOfVertices();
cout << "\n边的条数为：" << f.NumOfEdges();
cout << "\n深度优先搜索序列为：";
f.DepthFirstSearch();
cout << "\n广度优先搜索序列为：";
f.BroadFirstSearch();
return ;
}
最终结果
c++实验9 图及图的操作实验的更多相关文章
- OpenCV 图象腐蚀形态学操作 全家桶
图象腐蚀与形态学操作 opencv 1. 通过调用库函数实现图像的腐蚀.膨胀: 2. 通过设置结构元素.元素大小.形态学操作类型实现对图象的形态学操作. 源码(VS2017+OpenCV 4.0) # ...
- 使用 DML语句，对 “锦图网” 数据进行操作，连接查询（内连接，左外连接，右外连接，全连接）
查看本章节 查看作业目录 需求说明: 对 "锦图网" 数据进行操作: 统计每一种线路类型的线路数量.最高线路价格.最低线路价格和平均线路价格,要求按照线路数量和平均线路价格升序显示 ...
- 使用 DML语句，对 “锦图网” 数据进行操作，聚合函数练习
查看本章节 查看作业目录 需求说明: 根据客户 ID 统计订单数.订单总金额.最高订单金额.最低订单金额和每份订单平均金额,并按订单总金额升序显示 根据客户统计订单总订购人次数> 5 的统计信息 ...
- UML九种图-包图、类图
UML九种图-包图.类图 一.包 (一)相关概念: 1.包: 一个包=一层=一个命名空间=一个文件夹 2.包的命名: 简单名:王老二 路径名:中国.河北省.廊坊市.廊坊师范学院.信息技术提高班.九期班 ...
- 如何增强ArcGIS插值图出图效果
如何增强ArcGIS插值图出图效果 by 李远祥 在一些科研领域,经常会遇到使用插值的方式进行处理,并生成最终的插值图.插值图在ArcGIS里面非常容易生成,只要具备了采用点数据,通过ArcToolB ...
- 【UML 建模】UML建模语言入门 -- 静态图详解 类图 对象图 包图 静态图建模实战
发现个好东西思维导图, 最近开始用MindManager整理博客 . 作者 :万境绝尘 转载请注明出处 : http://blog.csdn.net/shulianghan/article/deta ...
- 【Excel】绘图案例_常见复合图：簇状图+堆积图+折线图
前言 最近有朋友让我帮忙用excel画图,老实说我很讨厌用excel画图,点来点去,复杂一些还不能复用,非常繁琐.当然,入门也很简单.需求时不同城市.不同产品的2016和2017销量及环比数据,这应该 ...
- R & ggplot2 & Excel绘图（直方图/经验分布图/QQ图/茎叶图/箱线图）实例
持续更新~ 散点图 条形图 文氏图 饼图 盒型图 频率直方图 热图 PCA图 3D图 火山图 分面图 分面制作小多组图 地图 练习数据: year count china Ame jap '12 2. ...
- UML建模语言入门 -- 静态图详解 类图 对象图 包图 静态图建模实战
发现个好东西思维导图, 最近开始用MindManager整理博客 . 作者 :万境绝尘 转载请注明出处 : http://blog.csdn.net/shulianghan/article/deta ...
随机推荐
- HTML-简单动画
简单动画 (1)简单动画通常称之为“过渡transition” Transition-property:需要过渡的属性,但是并非所有的属性都支持过渡. Transition-duration:过渡的时 ...
- 81. Search in Rotated Sorted Array II (JAVA)
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e. ...
- 查询GC日志、动态年龄计算
https://www.cnblogs.com/onmyway20xx/p/6590603.html 从实际案例聊聊Java应用的GC优化 动态年龄计算 关于上文中提到晋升年龄阈值为2,很多同学有疑问 ...
- Python3使运行暂停的方法
在Python3中已经有很大一部分语句与Python2不互通了,运行暂停的方法也有所不同. 1.input(); 这种方法不用包含模块,因此这也是最常用的一种暂停手段. Python2中的raw_in ...
- Matlab 快速多通道积分图计算函数
所谓快速多通道积分图计算,其实就是 cumsum2D. 我写了一个比较快的版本(比 VLFeat 的快),用 mex 编译一下就能用了. 代码 #include <string.h> #i ...
- Laravel配置全局公共函数的方法步骤
前言 在laravel项目开发中,经常使用到公共函数,那如何在laravel配置全局公共函数呢??下面话不多说了,来一起看看详细的介绍吧 方法如下 在Laravel项目中我们常常需要定义一些全局的公共 ...
- Linux部署Redis及PHP-redis扩展
Redis是一个key-value存储系统,属于我们常说的NoSQL.它遵守BSD协议.支持网络.可基于内存亦可持久化的日志型.Key-Value数据库,并提供多种语言的API.它常用在缓存.队列.P ...
- linux编译安装mysql5.7
一.下载源码包 -src cd /usr/local/src/mysql--src wget https://dev.mysql.com/get/Downloads/MySQL-5.7/mysql-5 ...
- Big Data（一）分治思想
按照课程安排,接下来半年,我将会去上一个为期半年的大数据课程.第一课是马士兵老师机构的周老师所讲,这里单纯记录讲课的内容. 问题1: 我有一万个元素(比如数字或单词)需要存储? 如果查找某一个元素,最 ...
- ASP.NET 中 取得 Repeater 里的checkbox值
前言:这两天在维护ASP.NET的项目,需要做一个checkbox来选择数据进行导出,下面提供两种解决思路 1.ASP:CheckBox asp:CheckBox自带控件,没有Value值 <a ...