机器学习-非线性回归(Logistic Regression)及应用

1. 概率

1.1 定义：概率(Probability):对一件事情发生的可能性的衡量。

1.2 范围：0 <= P <= 1

1.3 计算方法：

1.3.1 根据个人置信

1.3.2 根据历史数据

1.3.3 根据模拟数据

1.4 条件概率：

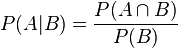
2. Logistic Regression(逻辑回归)

2.1 列子：模拟癌症肿瘤是良性还是恶性

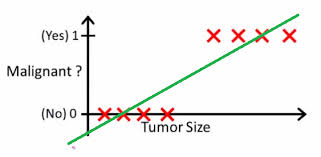
h(x) > 0.5

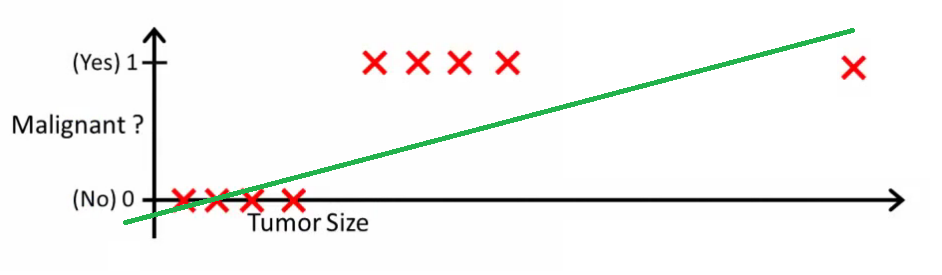
h(x) > 0.2

2.2 基本模型

测试数据为：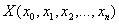

要学习的参数为：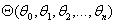

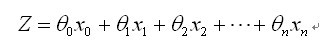
向量表示：

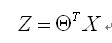
由于y取值在[0,1]之间，所有需要处理二值数据，引入Sigmoid函数来使得曲线平滑化

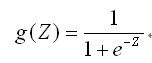
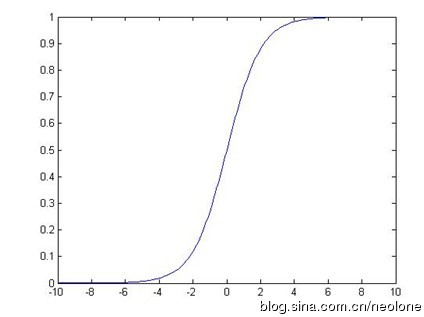
预测函数：

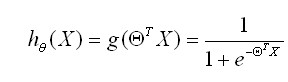
用概率表示：

正例(y = 1):

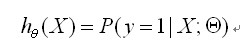
反例(y = 0):

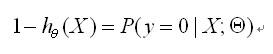
2.3 Cost函数

线性回归：

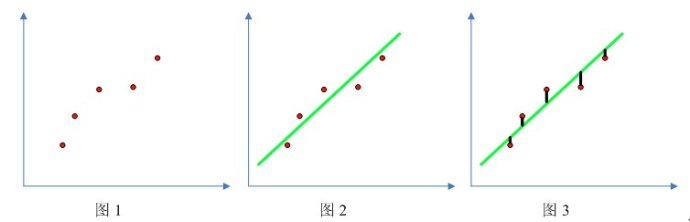
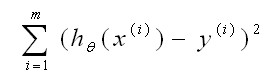(预测值-实例值)

(类似于线性模型)

在简单线性模型中找到合适的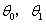使得上式最小

Logistic regression:

Cost函数：

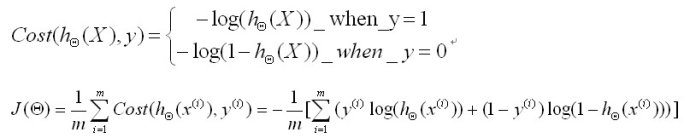
上式合并可以得到下面的式子

目标：找到合适的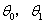使得上式最小

2.4 解法：梯度下降法(gradient decent)

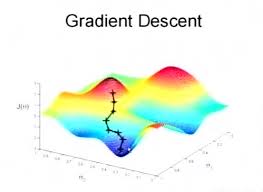
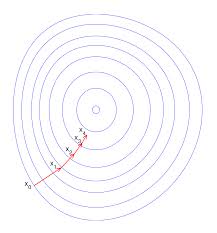
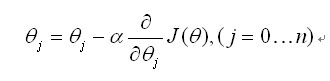
为学习率

更新法则：

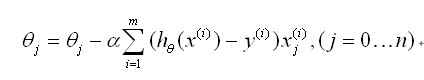
为学习率

同时对所有的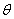进行更新，重复更新知道收敛

# -*- coding:utf-8 -*-

import numpy as np
import random

#产生模拟数据 numPoints实例个数  bias偏好值 variance方差
def genData(numPoints, bias, variance):
    x = np.zeros(shape=(numPoints, 2))
    y = np.zeros(shape=(numPoints)) #1行 如：1x100
    for i in range(0, numPoints):#每一行循环
        x[i][0] = 0 #每行第一列等于1
        x[i][1] = i #每行第二列等于i
        y[i] = (i + bias) + random.uniform(0, 1) + variance
    return x,y

#梯度下降
def gradientDescent(x, y, theta, alpha, m, numIterations): #alpha学习率 m实例个数 numIterations更新次数
    xTran = np.transpose(x)#转置
    for i in range(numIterations):
        hypothesis = np.dot(x, theta)#估计值
        loss = hypothesis - y#估计值-实际值
        cost = np.sum(loss**2)/(2*m)#这里的定义最简单的cost函数和实际定义有出入
        gradient = np.dot(xTran,loss)/m#更新量
        theta = theta - alpha*gradient
        print("Iteration %d | cost: %f" %(i, cost))
    return theta

#测试
x, y = genData(100, 25, 10)
# print("x:")
# print(x)
# print("y:")
# print(y)
#
m, n = np.shape(x)
n_y = np.shape(y)
#
# print("x_shape:" ,str(m)," ",str(n))
# print("y_shape:" , str(n_y))

numIterations = 100000
alpha = 0.0005
theta = np.ones(n)
theta = gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)