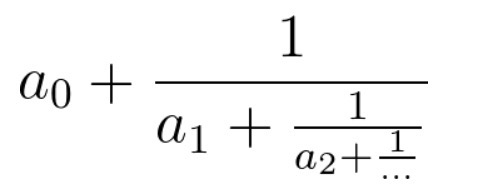【leetcode】LCP 2. 分式化简
题目如下:
有一个同学在学习分式。他需要将一个连分数化成最简分数,你能帮助他吗?
连分数是形如上图的分式。在本题中,所有系数都是大于等于0的整数。
输入的cont代表连分数的系数(cont[0]代表上图的a0,以此类推)。返回一个长度为2的数组[n, m],使得连分数的值等于n / m,且n, m最大公约数为1。
示例 1:
输入:cont = [3, 2, 0, 2]
输出:[13, 4]
解释:原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。示例 2:
输入:cont = [0, 0, 3]
输出:[3, 1]
解释:如果答案是整数,令分母为1即可。限制:
cont[i] >= 0
1 <= cont的长度 <= 10
cont最后一个元素不等于0
答案的n, m的取值都能被32位int整型存下(即不超过2 ^ 31 - 1)。
解题思路:题目不难,用两个变量分别记录分子和分母的值,从后往前计算cont,每次计算完成后交换分子和分母的值即可。
代码如下:
class Solution(object):
def fraction(self, cont):
"""
:type cont: List[int]
:rtype: List[int]
"""
rc = cont[::-1]
numerator = rc[0]
denominator = 1
for i in range(1,len(rc)):
numerator, denominator = denominator, numerator
numerator += rc[i] * denominator
return [numerator,denominator]
【leetcode】LCP 2. 分式化简的更多相关文章
- HDU.2503 a/b + c/d (分式化简)
a/b + c/d Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- LCP 2-分式化简
LCP 2-分式化简 public int[] fraction(int[] cont) { int len = cont.length; int[] d = new int[]{cont[len - ...
- YZOI Easy Round 2_化简(simplify.c/cpp/pas)
Description 给定一个多项式,输出其化简后的结果. Input 一个字符串,只含有关于字母x 的多项式,不含括号与分式,没有多余的空格. Output 一个字符串,化简后的多项式,按照次数从 ...
- 线性可分SVM中线性规划问题的化简
在网上找了许多关于线性可分SVM化简的过程,但似乎都不是很详细,所以凭借自己的理解去详解了一下. 线性可分SVM的目标是求得一个超平面(其实就是求w和b),在其在对目标样本的划分正确的基础上,使得到该 ...
- NOIP201402比例化简
比例化简 [问题描述]在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果.例如,对某一观点表示支持的有 1498 人,反对的有 902 人,那么赞同与反对的比例可以简单的记为1498:9 ...
- 【mongoDB高级篇②】大数据聚集运算之mapReduce(映射化简)
简述 mapReduce从字面上来理解就是两个过程:map映射以及reduce化简.是一种比较先进的大数据处理方法,其难度不高,从性能上来说属于比较暴力的(通过N台服务器同时来计算),但相较于grou ...
- 化简复杂逻辑,编写紧凑的if条件语句
当业务逻辑很复杂,涉及多个条件的真假,或者多种条件下都会执行同一动作时,如何编写紧凑的if语句呢?本文借由一个实际例子,利用数学的布尔逻辑整理条件,最终产生if语句. 问题 在<X3 重聚> ...
- 《Linear Algebra and Its Application》-chaper1-行化简法解决线性方程组
在实际生产生活中,需要我们解大量的线性方程组,例如是有探测.线性规划.电路等,这里我们便从理论角度建立一套解决线性方程组的体系. 线性方程组: 形如下面形式的方程组称为线性方程组. 回想起解决二元线性 ...
- poj3708:函数式化简+高精度进制转换+同余方程组
题目大意 给定一个函数 找出满足条件 等于 k 的最小的x m,k,d已知 其中 m,k 很大需要使用高精度存储 思路: 对 函数f(m)进行化简 ,令t=ceil( log(d,m) ) 可以得 ...
随机推荐
- 【DSP开发】【计算机视觉】EMCV:可在DSP上运行的OpenCV
EMCV:可在DSP上运行的OpenCV EMCV项目主页: http://sf.net/projects/emcv EMCV全称为Embedded Computer Vision Library,是 ...
- 【Linux开发】linux设备驱动归纳总结(六):2.分享中断号
linux设备驱动归纳总结(六):2.分享中断号 xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx ...
- DQN算法原理详解
一. 概述 强化学习算法可以分为三大类:value based, policy based 和 actor critic. 常见的是以DQN为代表的value based算法,这种算法中只有一个值函数 ...
- vue--vue-resource实现 get, post, jsonp请求
vue-resource 实现 get, post, jsonp请求 除了 vue-resource 之外,还可以使用 axios 的第三方包实现实现数据的请求 之前的学习中,如何发起数据请求? 常见 ...
- mybatis 基础(二) xml文件中的其他知识点
mybatis xml文件中一些标签的使用 此标签主要用作 配置 "别名" 如果实体类与数据库中字段名在不区分大小写的情况下相同的话, 那就不需要配置resultMap,因为mys ...
- 【一道来自老师的题的题解】equip——奇妙的最短路
这道题真的第一眼完全想不到是最短路啊!!!!!!!! 感谢DR大佬讲解!!!!!90°鞠躬 =u= 暂时没有评测网址,(因为需要special judge)敬请期待 机房另一大佬JYY题解,可以对比参 ...
- NOIP2017普及组比赛总结
期中考总结&NOIP2017总结 2017年11月11日,我第二次参加NOIP普及组复赛.上一年,我的得分是250分,只拿到了二等奖.我便把目标定为拿到一等奖,考到300分以上. 早上8点多, ...
- RuntimeError: Model class user.models.User doesn't declare an explicit app_label and isn't in an application in INSTALLED_APPS.
Django 2.x版本迁移数据库报这个错误,user表使用的Django的验证系统 本来就想改一下用户表的表名,莫名的报了个这个错误,在网上找到了解决办法 打开user应用模块下的apps.py文件 ...
- oracle 安装后参数调整
关闭11g 新特性 开归档 oracle 11g安装完成需修改:1.关闭审计alter system set audit_trail=none scope=spfile sid='*'; 防止ORA- ...
- Nginx(高并发)
Nginx(engine x)高性能和反向代理的web服务器反向代理:保护客户资源,只要是http协议都可以Web服务器:IIS 阿帕奇 NginxNginx可以作为负载均衡(NLB只支持Http)我 ...