js:数据结构笔记10--图和图算法

图：是由边和定点的集合组成；  按照图的定点对是否有序可以分为：有向图和无向图；

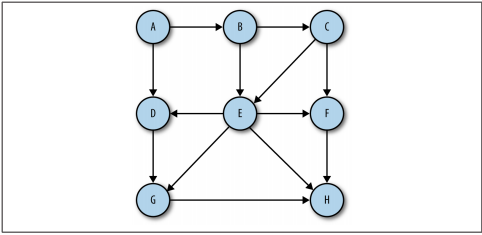
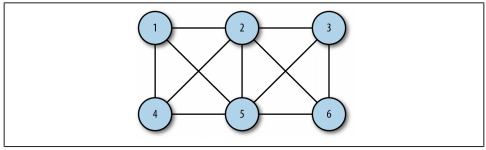
 路径：所有顶点都由边连接构成；路径长度为第一个定点到最后一个顶点之间的数量；

 环：指向自身的顶点，长度为0；圈：至少有一条边的路径，且第一个顶点和最后一个顶点相同；

强连通：如果两个顶点之间有路径，则这两个顶点就是强连通，反之；

构建简单有向图：

利用邻接表数组表示：构建二维数组，第一个存储顶点标号，第二个存储与这个顶点相连的顶点标号；

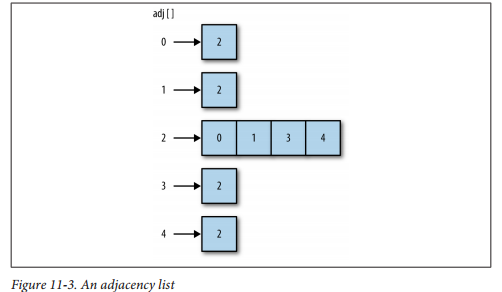
function Graph (v) {
	this.vertices = v; //顶点个数
	this.edges = 0;  //边条数
	this.adj = [];
	for(var i = 0; i < this.vertices; ++i) {
		this.adj[i] = [];  //二维数组
		//this.adj[i].push("");
	}
	this.addEdge = addEdge;
	this.showGraph = showGraph;
}
function addEdge(v,w) {  //构建边
	this.adj[v].push(w);
	this.adj[w].push(v);
	this.edges++;
}
function showGraph() {
	var str = "";
	for(var i = 0; i < this.vertices; ++i) {
		str = i + "-->";
		for(var j = 0; j < this.vertices; ++j) {
			if(this.adj[i][j] != undefined) {
				str += this.adj[i][j] + " ";
			}
		}
		console.log(str);
	}
}

　操作：demo:　

 搜索图：确定从一个指定顶点可以到达其他哪些顶点；注意：在更换顶点之后，图的树结构也要变化；

• 深度优先搜索：从一条路径开始知道最后一个顶点，然后回溯继续下一条路径，反复直到没有路径；
  • 查找与当前顶点相邻未访问的顶点，将其值输出，并在标记数组中将相应标号标记为true;
  • 依次重复；

function init() {
	for(var i = 0; i < this.vertices; ++i) {
		this.adj[i] = [];
		this.marked[i] = false;
	}
}
function dfs(v) {
	this.marked[v] = true;
	var adj = this.adj[v],nextAdj;
	if(adj != undefined) {
		console.log("Visited vertex: " + v);
	}
	for(var w in adj) {
		var nextAdj = this.adj[v][w];
		if(!this.marked[nextAdj]) {
			this.dfs(nextAdj);
		}

	}
}

操作：demo:

• 广度优先搜索：首先检查最靠近第一个顶点的层，然后逐层搜索；
  • 查找与当前顶点相邻未访问的顶点；将其添加到已访问列表；
  • 这一层访问之后从图中取出下一个顶点，添加到以访问列表；
  • 继续；

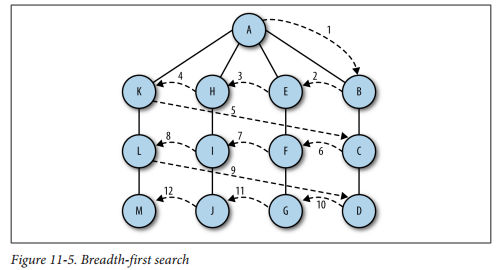
//在 Graph 中添加this.edgeTo = [];来记录哪个顶点访问到它，所以第一个会是undefined;

function dfs(s) {
	var queue = [],adj = this.adj[s],nextAdj;
	this.marked[s] = true;
	queue.push(s);
	while(queue.length > 0) {
		var v = queue.shift();
		if(v != undefined) {
			console.log("Visited vertex: " + v);
		}
		adj = this.adj[v];
		for(var w in adj) {
			var nextAdj = this.adj[v][w];
			if(!this.marked[nextAdj]) {
				this.edgeTo[nextAdj] = v;
				this.marked[nextAdj] = true;
				queue.push(nextAdj);
			}
		}

	}
}

操作：demo:

 查找最短路径：

广度优先搜索对应的最短路径：

function pathTo(s,v) { //from s to v;
	this.dfs(s);
	if(!this.hasPathTo(v)) {
	   return undefined;
	}
	var path = [];
	for(var i = v;i != s; i = this.edgeTo[i]) {
	   path.push(i);
	}
	path.push(s);
	this.printPath(path);
}
function hasPathTo(v) {
	return this.marked[v];
}
function printPath(paths) {
	var str = "";
	while(paths.length > 0) {
		if(paths.length > 1) {
			str += paths.pop() + "-";
		} else {
			str += paths.pop();
		}
	}
	console.log(str);
}

　操作：demo:

 拓扑排序：

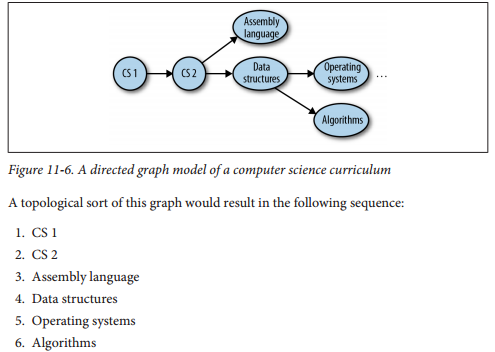
即优先级约束调度：在进行完1的时候才能开始2，之后可以同时开始3，4，以此类推；