codeforces 446C DZY Loves Fibonacci Numbers（数学 or 数论+线段树）（两种方法）

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are mqueries, each query has one of the two types:

1. Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
2. Format of the query "2 l r". In reply to the query you should output the value of 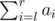 modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

题目大意：维护一个序列，每次给一段序列加上一个斐波那契数列，或者询问一段序列的和。

思路1：两个斐波那契的定理，用数学归纳法很容易证明：

①定义F[1] = a, F[2] = b, F[n] = F[n - 1] + F[n - 2]（n≥3）。有F[n] = b * fib[n - 1] + a * fib[n - 2]（n≥3），其中fib[i]为斐波那契数列的第 i 项。

②定义F[1] = a, F[2] = b, F[n] = F[n - 1] + F[n - 2]（n≥3）。有F[1] + F[2] + …… + F[n] = F[n + 2] - b。

这题还有一个事实，就是两个上述定义的数列，相加，仍然符合F[n] = F[n - 1] + F[n - 2]的递推公式。

利用这两个定理，用线段树维护序列，线段树的每个结点记录这一段的前两项是什么，预处理好斐波那契数列，便能O(1)地计算出每一个结点中间的数是多少、每一个结点的和。

代码（1513MS）：

 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cstdio>
 #include <cmath>
 using namespace std;
 typedef long long LL;
 #define ll (x << 1)
 #define rr ((x << 1) | 1)
 #define mid ((l + r) >> 1)

 const int MOD = 1e9 + ;

 const int MAXN = ;
 const int MAXT = MAXN << ;

 int f1[MAXT], f2[MAXT], sum[MAXT];
 int a[MAXN], fib[MAXN];
 int n, m;

 void init() {
     fib[] = fib[] = ;
     for(int i = ; i <= n + ; ++i) {
         fib[i] = fib[i - ] + fib[i - ];
         if(fib[i] >= MOD) fib[i] -= MOD;
     }
 }

 int get_fib(int a, int b, int n) {
     if(n == ) return a;
     if(n == ) return b;
     return (LL(b) * fib[n - ] + LL(a) * fib[n - ]) % MOD;
 }

 int get_sum(int a, int b, int n) {
     return (get_fib(a, b, n + ) - b + MOD) % MOD;
 }

 void add_fib(int x, int l, int r, int a, int b) {
     (f1[x] += a) %= MOD;
     (f2[x] += b) %= MOD;
     (sum[x] += get_sum(a, b, r - l + )) %= MOD;
 }

 void pushdown(int x, int l, int r) {
     add_fib(ll, l, mid, f1[x], f2[x]);
     add_fib(rr, mid + , r, get_fib(f1[x], f2[x], mid +  - l + ), get_fib(f1[x], f2[x], mid +  - l + ));
     f1[x] = f2[x] = ;
 }

 void maintain(int x) {
     sum[x] = (sum[ll] + sum[rr]) % MOD;
 }

 void build(int x, int l, int r) {
     if(l == r) {
         sum[x] = a[l];
     } else {
         build(ll, l, mid);
         build(rr, mid + , r);
         maintain(x);
     }
 }

 void update(int x, int l, int r, int a, int b) {
     if(a <= l && r <= b) {
         add_fib(x, l, r, fib[l - a + ], fib[l +  - a + ]);
     } else {
         pushdown(x, l, r);
         if(a <= mid) update(ll, l, mid, a, b);
         if(mid < b) update(rr, mid + , r, a, b);
         maintain(x);
     }
 }

 int query(int x, int l, int r, int a, int b) {
     if(a <= l && r <= b) {
         return sum[x];
     } else {
         int ret = ;
         pushdown(x, l, r);
         if(a <= mid) (ret += query(ll, l, mid, a, b)) %= MOD;
         if(mid < b) (ret += query(rr, mid + , r, a, b)) %= MOD;
         return ret;
     }
 }

 int main() {
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; ++i) scanf("%d", &a[i]);
     init();
     build(, , n);
     int op, l, r;
     while(m--) {
         scanf("%d%d%d", &op, &l, &r);
         if(op == ) update(, , n, l, r);
         if(op == ) printf("%d\n", query(, , n, l, r));
     }
 }

思路2：按官方题解的说法，有通项公式$ fib_n = \frac{ \sqrt 5 } 5 * (( \frac {1 + \sqrt 5} 2) ^ n - ( \frac {1 - \sqrt 5} 2) ^ n) $。

5是1e9+9的二次剩余，383008016^2=5(mod 1e9+9)。

利用逆元，可计算出：$ \frac {\sqrt 5} 5、\frac {1 + \sqrt 5} 2、 \frac {1 - \sqrt 5} 2 $在模1e9+9意义下的值。

然后，变成用线段树维护两个等比数列。预处理出$\frac {1 + \sqrt 5} 2$和$\frac {1 - \sqrt 5} 2$的1~n的次方的值，设他们为q，还要求出1-q的逆元（用于计算等比数列的和）。

线段树每个结点记录两个等比数列的首项，跟上面的方法差不多，也是这样维护一个线段树即可。

代码（1996MS）：

 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cstdio>
 #include <cmath>
 using namespace std;
 typedef long long LL;
 #define ll (x << 1)
 #define rr ((x << 1) | 1)
 #define mid ((l + r) >> 1)

 const int MOD = 1e9 + ;
 const int SQRT5 = ;

 const int MAXN = ;
 const int MAXT = MAXN << ;

 int powa[MAXN], powb[MAXN];
 int coe, ta, tb, invta, invtb;
 int fa[MAXT], fb[MAXT], sum[MAXT];
 int a[MAXN];
 int n, m;

 int inv(int x) {
     if(x == ) return ;
     return (LL(MOD - MOD / x) * inv(MOD % x)) % MOD;
 }

 void init() {
     coe = inv(SQRT5);
     ta = (LL( + SQRT5) * inv()) % MOD;
     tb = (LL( - SQRT5 + MOD) * inv()) % MOD;
     invta = inv( - ta + MOD);
     invtb = inv( - tb + MOD);
     //cout<<coe<<endl<<ta<<endl<<tb<<endl;
     powa[] = powb[] = ;
     for(int i = ; i <= n; ++i) {
         powa[i] = LL(powa[i - ]) * ta % MOD;
         powb[i] = LL(powb[i - ]) * tb % MOD;
     }
 }

 void maintain(int x) {
     sum[x] = (sum[ll] + sum[rr]) % MOD;
 }

 void add_fib(int x, int l, int r, int a, int b) {
     (fa[x] += a) %= MOD;
     (fb[x] += b) %= MOD;
     (sum[x] += LL(a) * ( - powa[r - l + ] + MOD) % MOD * invta % MOD) %= MOD;
     (sum[x] -= LL(b) * ( - powb[r - l + ] + MOD) % MOD * invtb % MOD) %= MOD;
     if(sum[x] < ) sum[x] += MOD;
 }

 void pushdown(int x, int l, int r) {
     add_fib(ll, l, mid, fa[x], fb[x]);
     add_fib(rr, mid + , r, LL(fa[x]) * powa[mid +  - l] % MOD, LL(fb[x]) * powb[mid +  - l] % MOD);
     fa[x] = fb[x] = ;
 }

 void build(int x, int l, int r) {
     if(l == r) {
         sum[x] = a[l];
     } else {
         build(ll, l, mid);
         build(rr, mid + , r);
         maintain(x);
     }
 }

 void update(int x, int l, int r, int a, int b) {
     if(a <= l && r <= b) {
         add_fib(x, l, r, LL(coe) * powa[l - a + ] % MOD, LL(coe) * powb[l - a + ] % MOD);
     } else {
         pushdown(x, l, r);
         if(a <= mid) update(ll, l, mid, a, b);
         if(mid < b) update(rr, mid + , r, a, b);
         maintain(x);
     }
 }

 int query(int x, int l, int r, int a, int b) {
     if(a <= l && r <= b) {
         return sum[x];
     } else {
         int ret = ;
         pushdown(x, l, r);
         if(a <= mid) (ret += query(ll, l, mid, a, b)) %= MOD;
         if(mid < b) (ret += query(rr, mid + , r, a, b)) %= MOD;
         return ret;
     }
 }

 int main() {
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; ++i) scanf("%d", &a[i]);
     init();
     build(, , n);
     int op, l, r;
     while(m--) {
         scanf("%d%d%d", &op, &l, &r);
         if(op == ) update(, , n, l, r);
         if(op == ) printf("%d\n", query(, , n, l, r));
     }
 }