数学工具（三）scipy中的优化方法

给定一个多维函数，如何求解全局最优？
文章包括：
1.全局最优的求解：暴力方法
2.全局最优的求解：fmin函数
3.凸优化

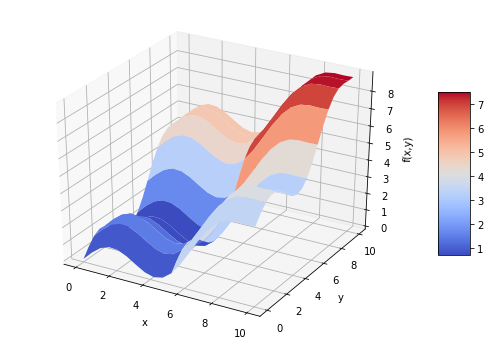
函数的曲面图
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

def fm(x,y):
return np.sin(x)+0.05*x**2+np.sin(y)+0.05*y**2

x = np.linspace(0, 10, 20)
y = np.linspace(0, 10, 20)
X, Y = np. meshgrid( x, y)

Z = fm(X,Y)
x = x.flatten()
y = x.flatten()

fig = plt.figure(figsize=(9,6))
ax =fig.gca(projection='3d')
surf = ax.plot_surface(X, Y, Z, rstride=2,cmap=mpl.cm.coolwarm,linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
fig.colorbar(surf , shrink=0.5, aspect=5)

1.全局最优的求解：暴力方法

import scipy.optimize as spo

def fo(p):
x,y=p
z= np.sin(x)+0.05*x**2+np.sin(y)+0.05*y**2
return z

rranges=(slice(-10,10.1,0.1),slice(-10,10.1,0.1))
res=spo.brute(fo,rranges,finish=None)
res

array([-1.4, -1.4])

全局最小值
fo(res)
-1.7748994599769203
对于更大的网格方位,scipy.optimize.brute() 变得非常慢。scipy.optimize.anneal() 提供了一个替代的算法，使用模拟退火，效率更高。

2.全局最优的求解：fmin函数

re=spo.fmin(fo,res,xtol=0.001, ftol=0.001, maxiter=15, maxfun=20)
re

array([-1.42702972, -1.42876755])

fo(re)
-1.7757246992239009

更一般的，我们一般传递两个参数：
re1=spo.fmin(fo,(2,2),maxiter=150)
re1

Optimization terminated successfully.
Current function value: 0.015826
Iterations: 46
Function evaluations: 86
Out[92]:
array([ 4.2710728 , 4.27106945])

3.凸优化

有约束的优化
\[
\begin{alignat}{5}
\max \quad &z= -(0.5*\sqrt(w_1)+0.5*\sqrt(w_2)) &&\\
\mbox{s.t.} \quad & w_1=a*15+b*5 \tag{constraint 1}\\
& w_{2}=a*5+b*12\tag{constraint 2}\\
& 100 \geq a*10+b*10 \tag{constraint 3}\\
& a,b \geq0
\end{alignat}
\]

代码实现：
def fu(p):
a,b=p[0],p[1]
return -(0.5np.sqrt(15a+5b)+0.5np.sqrt(5a+12b))

cons = ({'type': 'ineq', 'fun': lambda p: 100- 10 * p[0] - 10 * p[1]},
{'type': 'ineq', 'fun': lambda p: 100- 10 * p[0] - 10 * p[1]})
bnds=((0,1000),(0,1000))
x0=(3,5)
result=spo.minimize(fu,x0,method='SLSQP',bounds=bnds,constraints=cons)
result

fun: -9.700883561077609
jac: array([-0.48503506, -0.48508084])
message: 'Optimization terminated successfully.'
nfev: 32
nit: 8
njev: 8
status: 0
success: True
x: array([ 8.02744728, 1.97255272])

result['x']
array([ 8.02744728, 1.97255272])

result['fun']
-9.700883561077609