数据降维-LDA线性降维

1.什么是LDA？

LDA线性判别分析也是一种经典的降维方法，LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“*投影后类内方差最小，类间方差最大*”。

什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。
可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

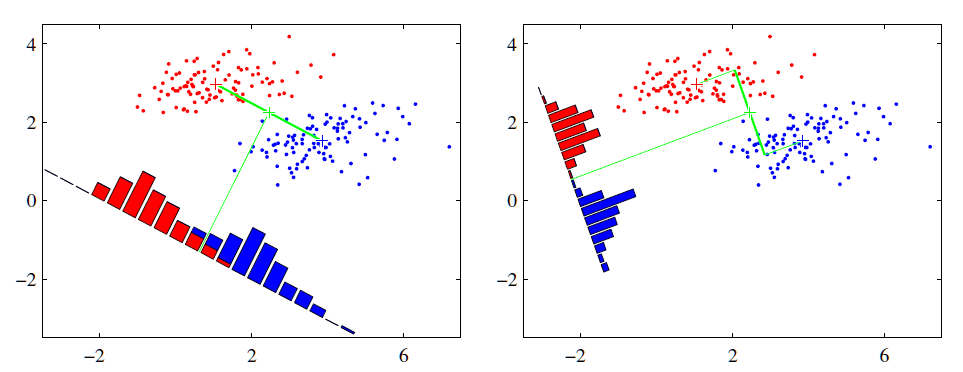
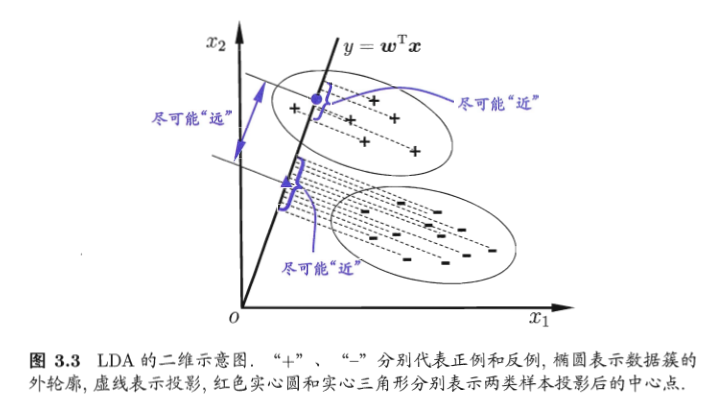
 2.LDA原理

 import numpy as np
 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
 from sklearn import datasets

 import warnings
 warnings.filterwarnings('ignore')

 X,y=datasets.load_iris(True)

 # 特征值和特征向量
 # solver是求解方法，svd表示奇异值分解
 lda = LinearDiscriminantAnalysis(solver='svd',n_components=2)
 X_lda = lda.fit_transform(X,y)
 X_lda[:5]

 # 1、总的散度矩阵
 # 协方差
 St = np.cov(X.T,bias = 1)

 # 2、类内的散度矩阵
 # Scatter散点图，within（内）
 Sw = np.full(shape = (4,4),fill_value=0,dtype=np.float64)
 for i in range(3):
     Sw += np.cov(X[y == i],rowvar = False,bias = 1)
 Sw/=3

 # 3、计算类间的散度矩阵
 # Scatter  between
 Sb = St - Sw

 # 4、特征值，和特征向量
 eigen,ev = linalg.eigh(Sb,Sw)
 display(eigen,ev)
 ev = ev[:, np.argsort(eigen)[::-1]]

 # 5、删选特征向量，进行矩阵运算
 X.dot(ev)[:,:2]

计算得到的结果：

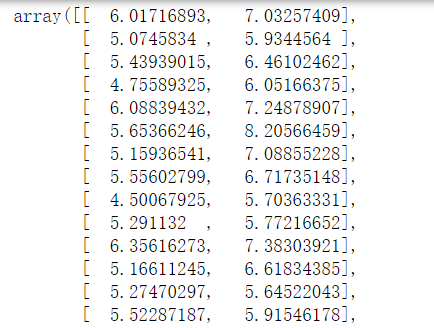
3.使用

使用和其他都一样，注意参数的含义

4.比较PCA和LDA

相同点：

1）两者均可以对数据进行降维。

2）两者在降维时均使用了矩阵特征分解的思想。

3）两者都假设数据符合高斯分布【正态分布】。

不同点：

1）LDA是有监督的降维方法，而PCA是无监督的降维方法

2）LDA降维最多降到类别数**k-1**的维数，而PCA没有这个限制。

3）LDA除了可以用于降维，还可以用于分类。

4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

5.机器学习中的监督学习和无监督学习

监督学习：

从给定的训练数据集中学习出一个函数（模型参数），当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集要求包括输入输出，也可以说是特征和目标。训练集中的目标是由人标注的。

常见的有监督学习算法：回归分析和统计分类。最典型的算法是KNN和SVM。

无监督学习：

输入数据没有被标记，也没有确定的结果。样本数据类别未知，需要根据样本间的相似性对样本集进行分类（聚类，clustering）试图使类内差距最小化，类间差距最大化。通俗点将就是实际应用中，不少情况下无法预先知道样本的标签，也就是说没有训练样本对应的类别，因而只能从原先没有样本标签的样本集开始学习分类器设计。

无监督学习的方法分为两大类：

(1)一类为基于概率密度函数估计的直接方法：指设法找到各类别在特征空间的分布参数，再进行分类。

(2)另一类是称为基于样本间相似性度量的简洁聚类方法：其原理是设法定出不同类别的核心或初始内核，然后依据样本与核心之间的相似性度量将样本聚集成不同的类别。

利用聚类结果，可以提取数据集中隐藏信息，对未来数据进行分类和预测。应用于数据挖掘，模式识别，图像处理等。

PCA和很多deep learning算法都属于无监督学习。