A排列方案

递归实现排列型枚举

把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 n。

输出格式

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围

1≤n≤9

输入样例：

3

输出样例：

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

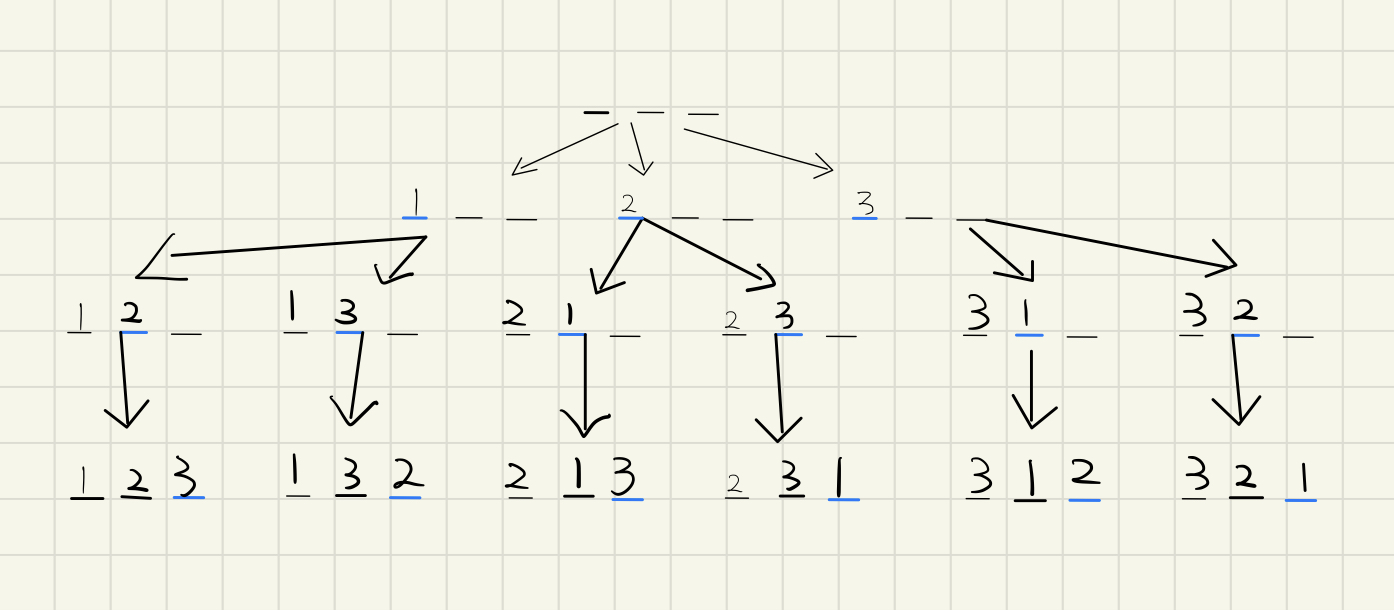
图解

Code

点击查看代码

#include<iostream>
using namespace std;
int n;
bool st[20];		//是否选过
int ways[20];		//保存方案

void dfs(int x){	//选到第x位
    if(x > n){		//选到第n+1位，即得到一种方案
        for(int i = 1; i <= n; i ++ ){		//输出方案
            cout << ways[i] << " ";
        }
        puts("");
    }

    for(int i = 1; i <= n; i ++ ){			//枚举每一位
        if(!st[i]){				//如果没选过
            st[i] = 1;
            ways[x] = i;		//选i
            dfs(x + 1);			//选下一位
			ways[x] = 0;		//恢复现场
            st[i] = 0;
        }
    }
}

int main(){
    cin >> n;
    dfs(1);			//从第一位开始选
}