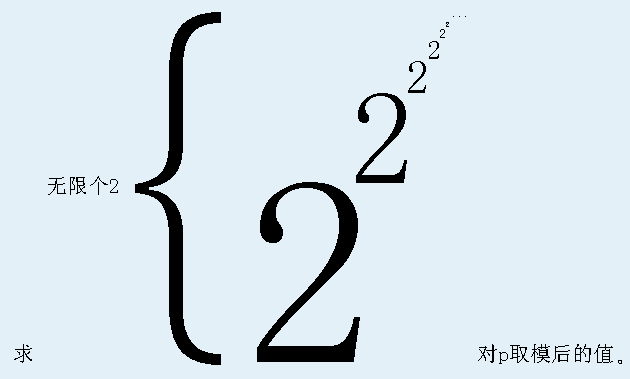BZOJ 3884 上帝与集合的正确用法
Description
根据一些书上的记载,上帝的一次失败的创世经历是这样的:
第一天, 上帝创造了一个世界的基本元素,称做“元”。
第二天, 上帝创造了一个新的元素,称作“\(\alpha\)”。“\(\alpha\)被定义为“元”构成的集合。容易发现,一共有两种不同的“\(\alpha\)”。
第三天, 上帝又创造了一个新的元素,称作“\(\beta\)”。“\(\beta\)”被定义为“\(\alpha\)”构成的集合。容易发现,一共有四种不同的“\(\beta\)”。
第四天, 上帝创造了新的元素“\(\gamma\)”,“\(\gamma\)”被定义为“\(\beta\)”的集合。显然,一共会有\(16\)种不同的“\(\gamma\)”。
如果按照这样下去,上帝创造的第四种元素将会有65536种,第五种元素将会有\(2^{65536}\)种。这将会是一个天文数字。
然而,上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来,因此,日复一日,年复一年,他重复地创造着新的元素……
然而不久,当上帝创造出最后一种元素“\(\theta\)”时,他发现这世界的元素实在是太多了,以致于世界的容量不足,无法承受。因此在这一天,上帝毁灭了世界。
至今,上帝仍记得那次失败的创世经历,现在他想问问你,他最后一次创造的元素“\(\theta\)”一共有多少种?
上帝觉得这个数字可能过于巨大而无法表示出来,因此你只需要回答这个数对\(p\)取模后的值即可。
你可以认为上帝从“\(\alpha\)”到“\(\theta\)”一共创造了\(10^{9}\)次元素,或\(10^{18}\)次,或者干脆\(\infty\)次。
一句话题意:
Input
接下来\(T\)行,每行一个正整数\(p\),代表你需要取模的值
Output
\(T\)行,每行一个正整数,为答案对\(p\)取模后的值
Sample Input
3
2
3
6
Sample Output
0
1
4
HINT
对于\(100\%\)的数据,\(T \le 1000,p \le 10^{7}\)
对于此题一个重要的定理:
当\(b \ge \phi(c)\)
\]
因为指数为无限项,恒有\(b \ge \phi(c)\),所以根据这个定理,我们就可以做题了。
令
\]
则有
\]
递归边界:
\]
所以这题就可以做了。
~~我深深感觉到了自己数学的弱菜,只知道定理却不会用。恶补数学ing~~
#include<cstdio>
#include<cstdlib>
#include<map>
using namespace std;
typedef long long ll;
map <int,int> M;
inline ll qsm(ll a,ll b,ll c)
{
ll ret = 1;
for (;b;b >>= 1,(a *= a)%=c)
if (b & 1) (ret *= a)%=c;
return ret;
}
inline ll phi(ll n)
{
ll ret = n;
for (ll i = 2;i*i <= n;++i)
{
if (n % i == 0)
{
while (n % i == 0) n /= i;
ret /= i; ret *= i-1;
}
}
if (n > 1) ret /= n,ret *= n-1;
return ret;
}
inline ll calc(ll n)
{
if (M.count(n)) return M[n];
ll p = phi(n);
return M[n] = qsm(2,calc(p)+p,n);
}
int main()
{
freopen("3884.in","r",stdin);
freopen("3884.out","w",stdout);
ll T; scanf("%lld",&T);
M[1] = 0;
while (T--)
{
ll n; scanf("%lld",&n);
printf("%lld\n",calc(n));
}
fclose(stdin); fclose(stdout);
return 0;
}
BZOJ 3884 上帝与集合的正确用法的更多相关文章
- bzoj 3884 上帝与集合的正确用法 指数循环节
3884: 上帝与集合的正确用法 Time Limit: 5 Sec Memory Limit: 128 MB[Submit][Status][Discuss] Description 根据一些 ...
- 【数学】[BZOJ 3884] 上帝与集合的正确用法
Description 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天, 上帝创造了一个世界的基本元素,称做“元”. 第二天, 上帝创造了一个新的元素,称作“α”.“α”被定义为“元” ...
- BZOJ 3884 上帝与集合的正确用法(扩展欧拉定理)
Description 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天, 上帝创造了一个世界的基本元素,称做“元”. 第二天, 上帝创造了一个新的元素,称作“α”.“α”被定义为“ ...
- bzoj 3884 上帝与集合的正确用法(递归,欧拉函数)
[题目链接] http://www.lydsy.com/JudgeOnline/problem.php?id=3884 [题意] 求2^2^2… mod p [思路] 设p=2^k * q+(1/0) ...
- BZOJ 3884: 上帝与集合的正确用法 [欧拉降幂]
PoPoQQQ大爷太神了 只要用欧拉定理递归下去就好了.... 然而还是有些细节没考虑好: $(P,2) \neq 1$时分解$P=2^k*q$的形式,然后变成$2^k(2^{(2^{2^{...}} ...
- BZOJ.3884.上帝与集合的正确用法(扩展欧拉定理)
\(Description\) 给定p, \(Solution\) 欧拉定理:\(若(a,p)=1\),则\(a^b\equiv a^{b\%\varphi(p)}(mod\ p)\). 扩展欧拉定理 ...
- 解题:BZOJ 3884 上帝与集合的正确用法
题面 好久以前写的,发现自己居然一直没有写题解=.= 扩展欧拉定理:在$b>φ(p)$时有$a^b \equiv a^{b\%φ(p)+φ(p)}(mod$ $p)$ 然后每次递归那个$a^{b ...
- BZOJ 3884: 上帝与集合的正确用法 扩展欧拉定理 + 快速幂
Code: #include<bits/stdc++.h> #define maxn 10000004 #define ll long long using namespace std; ...
- BZOJ 3884 上帝与集合的正确用法题解
一道智慧题 其实解这题需要用到扩展欧拉定理, 有了上面的公式,我们不难看出此题的解法. 设b为2^2^2^2^2.....显然,b要比φ(p)要大,所以可以直接套公式 modp时的答案 ans(p)= ...
随机推荐
- Ubuntu 14.04 没有system settings的解决方法
在我的Dell Latitude 3330上, 新装的Ubuntu 14.04一切正常,就是没有system settings程序, 以下的命令能够解决: sudo apt-get install u ...
- c++ timer基于win消息队列
能够承载10w个timer通信执行,说关闭就关闭,里面用了一个比較巧妙的线程处理,呵呵10W个timer就10多个线程,请大牛不要笑话,供新手学习之用 #pragma once #include &l ...
- flume学习安装
近期项目组有需求点击流日志须要自己收集,学习了一下flume而且成功安装了.相关信息记录一下. 1)下载flume1.5版本号 wget http://www.apache.org/dyn/clos ...
- gprof + kprof + gprof2dot (性能 与 函数调用图)-
http://www.cnblogs.com/rocketfan/archive/2009/11/15/1603465.html http://blog.csdn.net/stanjiang2010/ ...
- .Net4.0如何实现.NET4.5中的Task.Run及Task.Delay方法
前言 .NET4.0下是没有Task.Run及Task.Delay方法的,而.NET4.5已经实现,对于还在使用.NET4.0的同学来说,如何在.NET4.0下实现这两个方法呢? 在.NET4.0下, ...
- Android(java)学习笔记206:利用开源SmartImageView优化网易新闻RSS客户端
1.我们自己编写的SmartImageView会有很多漏洞,但是我们幸运的可以在网上利用开源项目的,开源项目中有很多成熟的代码,比如SmartImageView都编写的很成熟的 国内我们经常用到htt ...
- 运行yum报错:Error: Cannot retrieve metalink for repository: epel. Please verify its path
Error: Cannot retrieve metalink for repository: epel. Please verify its path and try again 当我们安装第三方扩 ...
- 用户输出表单处理php
php中的表单输入处理,我用两个文件,在linux输出: touch php_post1.html php_post1.php php_post1.html代码如下: <!doctype htm ...
- at91sam9x5 linux 4.1.0下使能蜂鸣器驱动
测试环境: CPU: AT91SAM9X35 Linux: Atmel提供的linux-at91-linux4sam_5.3 (Linux-4.1.0) 转载请注明: 凌云物网智科嵌入式实 ...
- Spring通过SchedulerFactoryBean实现调度任务的配置
http://blog.csdn.net/hu_shengyang/article/details/19815201(里面是配置) 介绍SchedulerFactoryBean http://blog ...