《A First Course in Probability》-chaper5-连续型随机变量-均匀随机变量

在连续随机变量这部分，有一种特殊的随机变量X，对于X所有可能取值，P(X)都相等，我们称其为均匀随机变量。

基于均匀随机变量的定义，我们容易看到，其密度函数f(x)必然是一条平行于x轴的直线，因为这样才能够保证如下等式成立。

对于X∈[a,b]的随机变量，我们能够直接得到其密度函数是f(x)=1/(b-a),x∈[a,b].

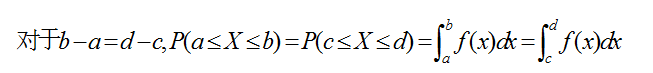
下面我们来看一个均匀随机变量的例子。

Q：向一个圆当中随机取一条弦，这条弦比该圆内接正三角形的边长要长的概率是多少？

分析：这其实是1889年法国数学家贝特朗提出的贝特朗悖论。

按照一般解决概率问题的策略，我们首相应该给出样本空间。

法一：样本空间Ω1={x|x为弦到圆心的距离}

法二：样本空间Ω2={x|x过弦端点的切线和弦围成的角度}

容易看到，对于不同的样本空间的定义方法，最终得到的结果是不同的。对于法一是1/2,对于法二的概率是1/3。

Q2(uva 12230):

给出A、B两点之间的距离，以及两点之间n条河的坐标、宽度以及该河上自动船的速度(河均与A、B两点连线垂直)，人在平地行进的速度是1，人从A到B所需的时间的期望(船的停泊完全随机)。

分析：这道问题基于期望的数学概念，突破口就是找到均匀分布这个分布模型。我们先从任意一条河分析起，过该条河的最短时间是L/v，也就是说已到达这条河的岸边，船也刚好到岸，而过该条河最长时间是3L/v，也就是说刚到达这条河的岸边，船刚好开走，也就是说设随机变量X表示过该条河的时间，那么X∈[L/v , 3L/v]，题目中又说船的停泊完全随机，因此X符合[L/v,3L/v]的均匀分布，那么易得，过该河的时间期望E[X]=2L/v.

对于剩余n-1条河的时间期望，采取相同的策略。再加上陆地上行走的时间D-sum(L)即可。