LinGo:装货问题——线性规划,整数规划,1988年美国数模B题
7种规格的包装箱要装有两辆铁路平板车上去，包装箱的宽和高相同，但厚度（t,以cm计）和重量（
以kg计）不同，
表A-1给出了每包装箱的厚度、重量和数量，每辆车有10.2m长的地方用来装包装箱（像面包片那样），车的载重为40吨，
对C5、C6、C7、规格的包装箱的总数有一个特殊的限制：这些规格箱子所占的空间（厚度）不能超过302.7cm。
试把包装箱装到两辆平板车上去（图A-6）使得浪费的空间最小。
表A-1 每种包装箱的厚度、重量和数量
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
|
|
t(cm) w(kg) n |
48.7 2000 8 |
52.0 3000 7 |
61.3 1000 9 |
72.0 500 6 |
48.7 4000 6 |
52.0 2000 4 |
64.0 1000 8 |
解：
一.设决策变量：
Xij表示第i辆平板车放j类包装箱Xij件
tj为第j个包装箱的厚度(cm)
wj为第j个包装箱的重量(kg)
nj表示第j个包装箱的数量
二.分析约束条件
1. 两辆车上的各种包装箱数量必须小于等于各类包装箱的总数
2.每辆车上的载重必须小于等于400000kg
3.每辆车上包装箱的长度必须小于等于1020cm
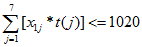
4. C5、C6、C7、规格的包装箱的总厚度不能超过302.7cm
5.包装箱的件数必须是整数
@for(link(i,j) : @gin(x(i,j)));
三.目标函数
[OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j));
四.LinGo代码
model:
sets:
row/../;
col/../ : t, w, n;
link(row, col) : x;
endsets data:
t = 48.7, 52.0, 61.3, 72.0, 48.7, 52.0, 64.0;
w = , , , , , , ;
n = , , , , , , ;
enddata @for(col(j) : @sum(row(i) : x(i,j)) <= n(j)); @for(row(i) : @sum(col(j) : x(i,j)*w(j)) <= ); @for(row(i) : @sum(col(j) : x(i,j)*t(j)) <= ); @sum(row(i) : @sum(col(j) | j#ge# : x(i,j) * t(j) )) <= 302.7; @for(link(i,j) : @gin(x(i,j))); [OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j)); end
五.LinGo运算结果
Global optimal solution found.
Objective value: 0.6000000
Objective bound: 0.6000000
Infeasibilities: 0.000000
Extended solver steps: 9342
Total solver iterations: 40250
Variable Value Reduced Cost
T( 1) 48.70000 0.000000
T( 2) 52.00000 0.000000
T( 3) 61.30000 0.000000
T( 4) 72.00000 0.000000
T( 5) 48.70000 0.000000
T( 6) 52.00000 0.000000
T( 7) 64.00000 0.000000
W( 1) 2000.000 0.000000
W( 2) 3000.000 0.000000
W( 3) 1000.000 0.000000
W( 4) 500.0000 0.000000
W( 5) 4000.000 0.000000
W( 6) 2000.000 0.000000
W( 7) 1000.000 0.000000
N( 1) 8.000000 0.000000
N( 2) 7.000000 0.000000
N( 3) 9.000000 0.000000
N( 4) 6.000000 0.000000
N( 5) 6.000000 0.000000
N( 6) 4.000000 0.000000
N( 7) 8.000000 0.000000
X( 1, 1) 8.000000 -48.70000
X( 1, 2) 1.000000 -52.00000
X( 1, 3) 0.000000 -61.30000
X( 1, 4) 6.000000 -72.00000
X( 1, 5) 3.000000 -48.70000
X( 1, 6) 0.000000 -52.00000
X( 1, 7) 0.000000 -64.00000
X( 2, 1) 0.000000 -48.70000
X( 2, 2) 6.000000 -52.00000
X( 2, 3) 9.000000 -61.30000
X( 2, 4) 0.000000 -72.00000
X( 2, 5) 0.000000 -48.70000
X( 2, 6) 3.000000 -52.00000
X( 2, 7) 0.000000 -64.00000
Row Slack or Surplus Dual Price
1 0.000000 0.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
5 3.000000 0.000000
6 1.000000 0.000000
7 8.000000 0.000000
8 366000.0 0.000000
9 367000.0 0.000000
10 0.3000000 0.000000
11 0.3000000 0.000000
12 0.6000000 0.000000
OBJ 0.6000000 -1.000000
结论：
浪费空间最小为：0.6cm
C1 C2 C3 C4 C5 C6 C7
第一辆 8 1 0 6 3 0 0
第二辆 0 6 9 0 0 3 0
LinGo:装货问题——线性规划,整数规划,1988年美国数模B题的更多相关文章
- Python数模笔记-Scipy库（1）线性规划问题
1.最优化问题建模 最优化问题的三要素是决策变量.目标函数和约束条件. (1)分析影响结果的因素是什么,确定决策变量 (2)决策变量与优化目标的关系是什么,确定目标函数 (3)决策变量所受的限制条件是 ...
- LinGo:疏散问题——线性规划,0-1规划
个部门(A.B.C.D.E)组成.现要将它的几个部门迁出甲市,迁至乙市或丙市. (每个城市最多接纳三个部门) 除去因政府鼓励这样做以外,还有用房便宜,招工方便等好处.对这些好处已作出数量估计,其值如下 ...
- LinGo:投资问题——线性规划
一.根据题目所给数据,建立一张表格方便查看 项目A 项目B 项目C 项目D 可投资年 1,2,3,4 3 2 1,2,3,4,5 收回本利年 次年年末 第5年 第5年 当年年末 本利 1.06 1.1 ...
- Python数模笔记-PuLP库（1）线性规划入门
1.什么是线性规划 线性规划(Linear programming),在线性等式或不等式约束条件下求解线性目标函数的极值问题,常用于解决资源分配.生产调度和混合问题.例如: max fx = 2*x1 ...
- 数模常用算法系列Matlab实现-----线性规划
线性规划的 Matlab 标准形式 线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号.为了避免这种形式多样性带来的不便,Matlab 中规定线性 规划的标 ...
- Python数模笔记-PuLP库（2）线性规划进阶
1.基于字典的创建规划问题 上篇中介绍了使用 LpVariable 对逐一定义每个决策变量,设定名称.类型和上下界,类似地对约束条件也需要逐一设置模型参数.在大规模的规划问题中,这样逐个定义变量和设置 ...
- 模拟退火算法Python编程（3）整数规划问题
1.整数规划问题 整数规划问题在工业.经济.国防.医疗等各行各业应用十分广泛,是指规划中的变量(全部或部分)限制为整数,属于离散优化问题(Discrete Optimization). 线性规划问题的 ...
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- Python小白的数学建模课-04.整数规划
整数规划与线性规划的差别只是变量的整数约束. 问题区别一点点,难度相差千万里. 选择简单通用的编程方案,让求解器去处理吧. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达 ...
随机推荐
- Day9 - Python 多线程、进程
Python之路,Day9, 进程.线程.协程篇 本节内容 操作系统发展史介绍 进程.与线程区别 python GIL全局解释器锁 线程 语法 join 线程锁之Lock\Rlock\信号量 将线 ...
- python的局部变量和全局变量
#coding=utf-8#全局变量与局部变量 #作用域def func(): i=8#print i# print object# j=9# print j #局部变量def func(a): i= ...
- exp、imp简单测试
imp 分为以下几个测试场景 imp name1/password1 file=xxxx.dmp full=y fromuser=name2 touser=name3 场景1 name1正确.pas ...
- JavaScript--模拟验证码
<!doctype html> <html> <head> <meta charset="UTF-8"> <title> ...
- [转载]Java synchronized详解
在编写一个类时,如果该类中的代码可能运行于多线程环境下,那么就要考虑同步的问题.在Java中内置了语言级的同步原语--synchronized,这也大大简化了Java中多线程同步的使用.我们首先编写一 ...
- Android入门随记
1.Activity是通过startActivity()开始的,结束后不反回任何结果,而用startActivityForResult(Intent intent, int resquestCode) ...
- 【USACO 2.2.1】序言页码
[题目描述] 一类书的序言是以罗马数字标页码的.传统罗马数字用单个字母表示特定的数值,以下是标准数字表: I 1 L 50 M 1000 V 5 C 100 X 10 D 500 最多3个同样的可以表 ...
- PHP获取函数返回值的引用
通过在函数前添加&可以获取函数返回值的引用,如:function &test(){return 10;}
- window.location.href问题，点击，跳转到首页
onClick="window.location.href='./';" 点击,跳转到首页. location.href=url Js中实现跳转 window.location.h ...
- Python学习笔记：02数据类型
Python 数据类型 python中标准的数据类型有 基础类型 整型(长整型) 浮点型 复数型 布尔型 序列类型 字符串 列表 元组 字典 整型 整型和长整型并不严格区分,整型int的表达范围和计算 ...