BZOJ 1509 逃学的小孩 - 树型dp

传送门

题目大意：

在一棵树中， 每条边都有一个长度值， 现要求在树中选择 3 个点 X、Y、 Z ， 满足 X 到 Y 的距离不大于 X 到 Z 的距离， 且 X 到 Y 的距离与 Y 到 Z 的距离之和最大，求这个最大值。

题目分析：

在一篇论文中看到了这道题，于是就来做做。

从这题中可以得到很多启示，光看题意一定会想到枚举点来做，不过如果枚举三点的话就爆了，于是枚举的那个点就成了解题的关键。我们发现，所有的答案无非就两种：

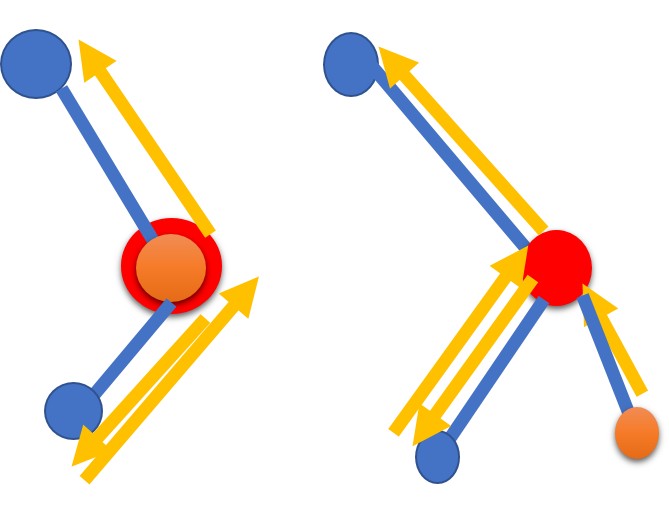
（红色代表特殊点，黄色代表起点）

他们都是最短路径 + 次短路径 * 2 + 最长路径（第一种情况相当于最短路径为0），于是第一种情况可以归到第二种情况中，这样一定是满足题意的条件下最优的。那么直接分析第二种情况：

发现无论是第一种还是第二种都有一个特殊点---分叉点A，如果用分叉点来表示距离那么|XY| + |YZ| = |XA| + 2|YA| + |ZA|，要让答案最大，也就是让三点到A的距离最大。

这下就好办了，求最大距离---树型dp：这样的三条链又有两种情况：



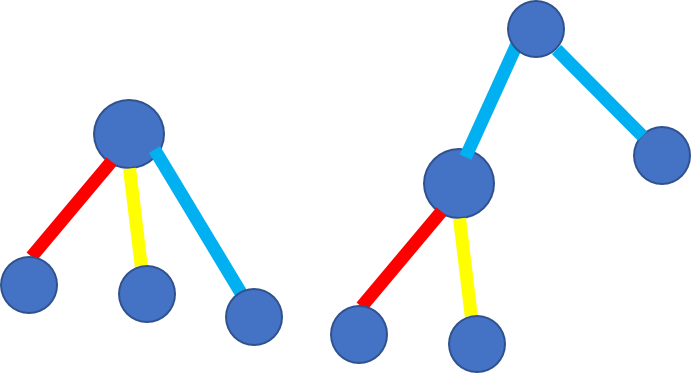
第一种是三条链都在子树中，第二种是一条在子树外，两条在子树中。那么进行两遍dp：第一遍从求u向下的三条不在同一颗子树的三条最长链（最长，次长，次次长），第二遍求u向上的一条最长链。

最后统计u分叉点的答案时，取这四条链的前三大，答案更新为最短路径 + 次短路径 * 2 + 最长路径。

改了我一个多小时，结果发现是输出优化的int没有改成long long！！

code

#include<bits/stdc++.h>
using namespace std;
#define maxn 200050
typedef long long ll;
namespace IO{
    inline int read(){
        int i = 0, f = 1; char ch = getchar();
        for(; (ch < '0' || ch > '9') && ch != '-'; ch = getchar());
        if(ch == '-') f = -1, ch = getchar();
        for(; ch >= '0' && ch <= '9'; ch = getchar())
            i = (i << 3) + (i << 1) + (ch - '0');
        return i * f;
    }
    inline void wr(ll x){
        if(x < 0) putchar('-'), x = -x;
        if(x > 9) wr(x / 10);
        putchar(x % 10 + '0');
    }
}using namespace IO;
int n, m;

typedef pair<int, ll> P;
vector<P> adj[maxn];
ll dp[maxn][5], ans;

inline void dfs1(int u, int f){
	for(int e = adj[u].size() - 1; e >= 0; e--){
		int v = adj[u][e].first;
		if(v == f) continue;
		ll t = adj[u][e].second;
		dfs1(v, u);
		if(dp[v][1] + t > dp[u][1]){
			dp[u][3] = dp[u][2];
			dp[u][2] = dp[u][1];
			dp[u][1] = dp[v][1] + t;
		}
		else if(dp[v][1] + t > dp[u][2]){
			dp[u][3] = dp[u][2];
			dp[u][2] = dp[v][1] + t;
		}
		else if(dp[v][1] + t > dp[u][3]){
			dp[u][3] = dp[v][1] + t;
		}
	}
}

inline void dfs2(int u, int f){
	for(int e = adj[u].size() - 1; e >= 0; e--){
		int v = adj[u][e].first;
		if(v == f) continue;
		ll t = adj[u][e].second;
		ll a = (dp[v][1] + t == dp[u][1]) ? (dp[u][2]): (dp[u][1]);
		dp[v][4] = max(a + t, dp[u][4] + t);
		dfs2(v, u);
	}
}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= m; i++){
		int x = read(), y = read(), t = read();
		adj[x].push_back(P(y, 1ll*t));
		adj[y].push_back(P(x, 1ll*t));
	}
	dfs1(1, 0);

	dfs2(1, 0);
	for(int i = 1; i <= n; i++){
		ll tmp[10];
		tmp[1] = dp[i][1], tmp[2] = dp[i][2], tmp[3] = dp[i][3], tmp[4] = dp[i][4];
		sort(tmp + 1, tmp + 4 + 1);
		ans = max(ans, tmp[2] + tmp[3]*2 + tmp[4]);
	}
	wr(ans);
	return 0;
}