洛谷——P1351 联合权值

https://www.luogu.org/problem/show?pid=1351

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1：

5
1 2
2 3
3 4
4 5
1 5 2 3 10 

输出样例#1：

20 74

说明

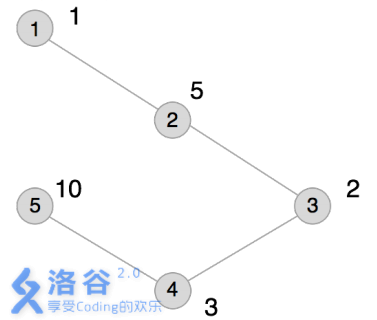
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

有点逆向思维的感觉——题目描述为距离为2的两点求值，那就可以枚举每个点所连出的每个点（有点绕），就简单了

 #include <algorithm>
 #include <cstdio>
 #include <vector>

 using namespace std;

 const int mod();
 const int N=+;
 vector<int>vec[N];
 int n,u,v,w[N];
 int s,maxn,ansmax,anssum;

 void work(int x)
 {
     int sum=,max1=,max2=;
     for(int i=;i<vec[x].size();i++)
     {
         if(w[vec[x][i]]>max1) max2=max1,max1=w[vec[x][i]];
         else
             if(w[vec[x][i]]>max2) max2=w[vec[x][i]];
         anssum=(anssum+sum*w[vec[x][i]])%mod;
         sum=(sum+w[vec[x][i]])%mod;
     }
     ansmax=max(ansmax,max1*max2);
 }

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<n;i++)
     {
         scanf("%d%d",&u,&v);
         vec[u].push_back(v);
         vec[v].push_back(u);
     }
     for(int i=;i<=n;i++) scanf("%d",w+i);
     for(int i=;i<=n;i++) work(i);
     printf("%d %d",ansmax,(anssum<<)%mod);
     return ;
 }