[数据结构]迪杰斯特拉（Dijkstra）算法

基本思想

通过Dijkstra计算图G中的最短路径时，需要指定起点vs(即从顶点vs开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点，而U则是记录还未求出最短路径的顶点(以及该顶点到起点vs的距离)。

初始时，S中只有起点vs；U中是除vs之外的顶点，并且U中顶点的路径是"起点vs到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，直到遍历完所有顶点。

操作步骤

(1) 初始时，S只包含起点vs；U包含除vs外的其他顶点，且U中顶点的距离为"起点vs到该顶点的距离"[例如，U中顶点v的距离为(vs,v)的长度，然后vs和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点vs的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(vs,v)的距离可能大于(vs,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

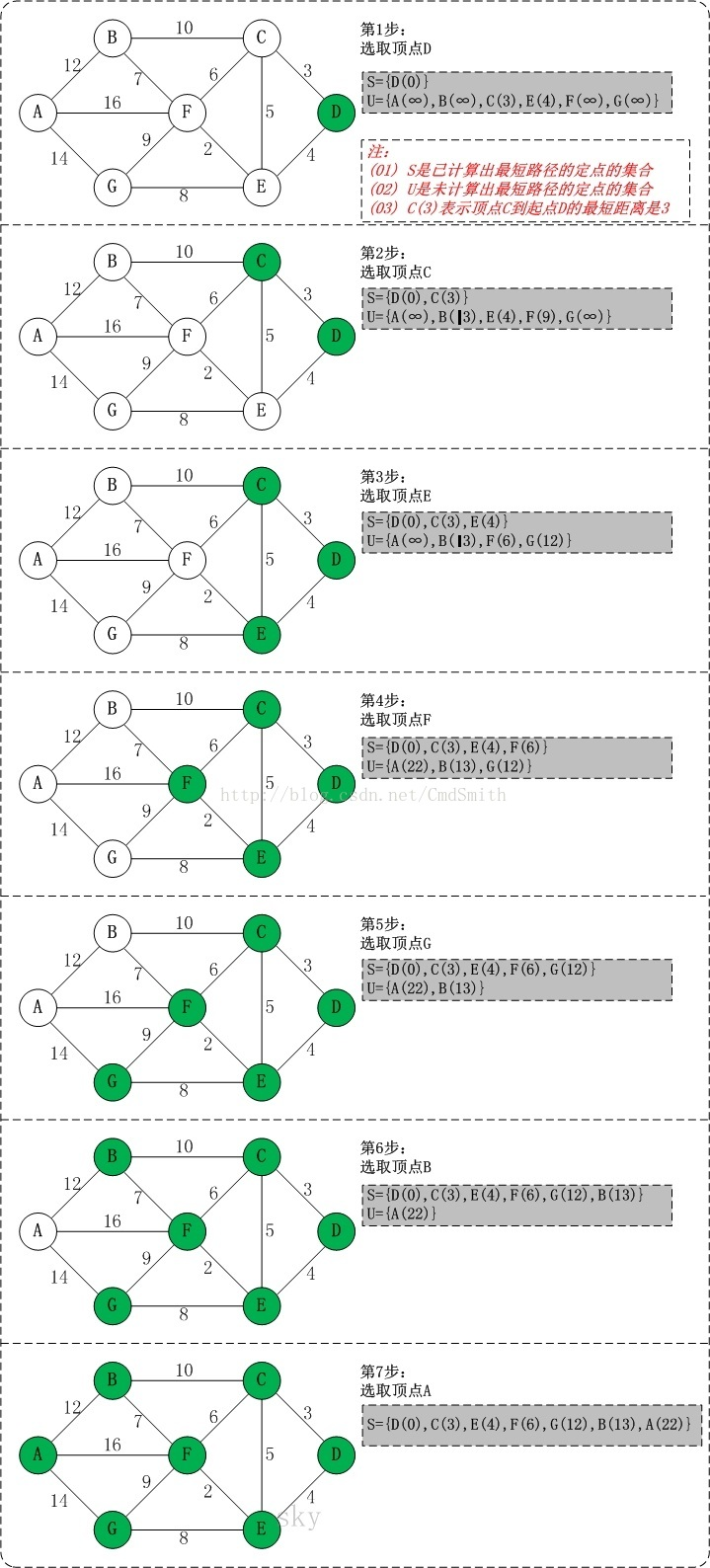
接下来做一个简单例子求解：

package com.darrenchan.graph;

import java.util.ArrayList;
import java.util.List;

public class ShortestPathDijkstra {
    /** 邻接矩阵 */
    private int[][] matrix;
    /** 表示正无穷 */
    private int MAX_WEIGHT = Integer.MAX_VALUE;
    /** 顶点集合 */
    private String[] vertexes;

    /**
     * 创建图
     */
    private void createGraph(int index) {
        matrix = new int[index][index];
        vertexes = new String[index];

        int[] v0 = { 0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
        int[] v1 = { 1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
        int[] v2 = { 5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
        int[] v3 = { MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT };
        int[] v4 = { MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT };
        int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT };
        int[] v6 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7 };
        int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4 };
        int[] v8 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 7, 4, 0 };
        matrix[0] = v0;
        matrix[1] = v1;
        matrix[2] = v2;
        matrix[3] = v3;
        matrix[4] = v4;
        matrix[5] = v5;
        matrix[6] = v6;
        matrix[7] = v7;
        matrix[8] = v8;

        vertexes[0] = "v0";
        vertexes[1] = "v1";
        vertexes[2] = "v2";
        vertexes[3] = "v3";
        vertexes[4] = "v4";
        vertexes[5] = "v5";
        vertexes[6] = "v6";
        vertexes[7] = "v7";
        vertexes[8] = "v8";
    }

    /**
     * Dijkstra最短路径。
     *
     * vs -- 起始顶点(start vertex) 即，统计图中"顶点vs"到其它各个顶点的最短路径。
     */
    public void dijkstra(int vs) {
        // flag[i]=true表示"顶点vs"到"顶点i"的最短路径已成功获取
        boolean[] flag = new boolean[vertexes.length];
        // U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)，与 flag配合使用,flag[i] == true 表示U中i顶点已被移除
        int[] U = new int[vertexes.length];
        // 前驱顶点数组,即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
        int[] prev = new int[vertexes.length];
        // S的作用是记录已求出最短路径的顶点
        String[] S = new String[vertexes.length];

        // 步骤一：初始时，S中只有起点vs；U中是除vs之外的顶点，并且U中顶点的路径是"起点vs到该顶点的路径"。
        for (int i = 0; i < vertexes.length; i++) {
            flag[i] = false; // 顶点i的最短路径还没获取到。
            U[i] = matrix[vs][i]; // 顶点i与顶点vs的初始距离为"顶点vs"到"顶点i"的权。也就是邻接矩阵vs行的数据。

            prev[i] = 0; //顶点i的前驱顶点为0
        }

        // 将vs从U中“移除”（U与flag配合使用）
        flag[vs] = true;
        U[vs] = 0;
        // 将vs顶点加入S
        S[0] = vertexes[vs];
        // 步骤一结束

        //步骤四：重复步骤二三，直到遍历完所有顶点。
        // 遍历vertexes.length-1次；每次找出一个顶点的最短路径。
        int k = 0;
        for (int i = 1; i < vertexes.length; i++) {
            // 步骤二：从U中找出路径最短的顶点，并将其加入到S中（如果vs顶点到x顶点还有更短的路径的话，那么
            // 必然会有一个y顶点到vs顶点的路径比前者更短且没有加入S中
            // 所以，U中路径最短顶点的路径就是该顶点的最短路径）
            // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
            int min = MAX_WEIGHT;
            for (int j = 0; j < vertexes.length; j++) {
                if (flag[j] == false && U[j] < min) {
                    min = U[j];
                    k = j;
                }
            }

            //将k放入S中
            S[i] = vertexes[k];

            //步骤二结束

            //步骤三：更新U中的顶点和顶点对应的路径
            //标记"顶点k"为已经获取到最短路径（更新U中的顶点，即将k顶点对应的flag标记为true）
            flag[k] = true;

            //修正当前最短路径和前驱顶点（更新U中剩余顶点对应的路径）
            //即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
            for (int j = 0; j < vertexes.length; j++) {
                //以k顶点所在位置连线其他顶点，判断其他顶点经过最短路径顶点k到达vs顶点是否小于目前的最短路径，是，更新入U，不是，不做处理
                int tmp = (matrix[k][j] == MAX_WEIGHT ? MAX_WEIGHT : (min + matrix[k][j]));
                if (flag[j] == false && (tmp < U[j])) {
                    U[j] = tmp;
                    //更新 j顶点的最短路径前驱顶点为k
                    prev[j] = k;
                }
            }
            //步骤三结束
        }
        //步骤四结束

        // 打印dijkstra最短路径的结果
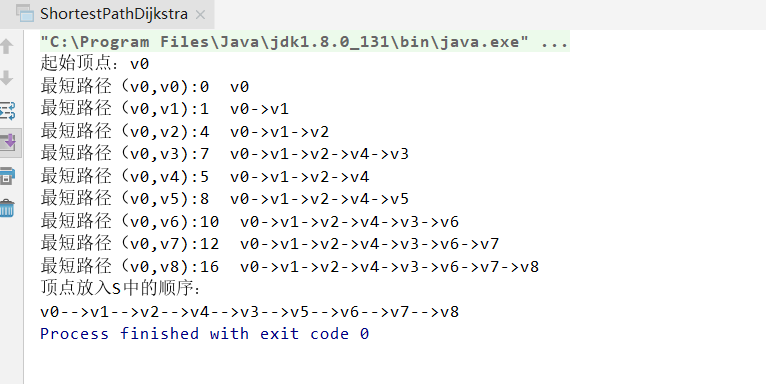
        System.out.println("起始顶点：" + vertexes[vs]);
        for (int i = 0; i < vertexes.length; i++) {
            System.out.print("最短路径（" + vertexes[vs] + "," + vertexes[i] + "):" + U[i] + "  ");

            List<String> path = new ArrayList<>();
            int j = i;
            while (true) {
                path.add(vertexes[j]);

                if (j == 0)
                    break;

                j = prev[j];
            }

            for (int x = path.size()-1; x >= 0; x--) {
                if (x == 0) {
                    System.out.println(path.get(x));
                } else {
                    System.out.print(path.get(x) + "->");
                }
            }

        }

        System.out.println("顶点放入S中的顺序：");
        for (int i = 0; i< vertexes.length; i++) {

            System.out.print(S[i]);

            if (i != vertexes.length-1)
                System.out.print("-->");
        }

    }

    public static void main(String[] args) {
        ShortestPathDijkstra dij = new ShortestPathDijkstra();
        dij.createGraph(9);
        dij.dijkstra(0);
    }

}

参考：https://blog.csdn.net/CmdSmith/article/details/56839285