boruvka算法

算法正确性证明：
1.最优性：最小边一定包含在生成树中。
2.合法性：一定不会构成环。如果存在环说明一个点的最小连边有两个，显然矛盾。

算法时间复杂度证明：
每执行一次算法，所有联通块的大小都至少为2，因此总联通块个数一定至少/2，因此最多只会执行log次。

算法实现：

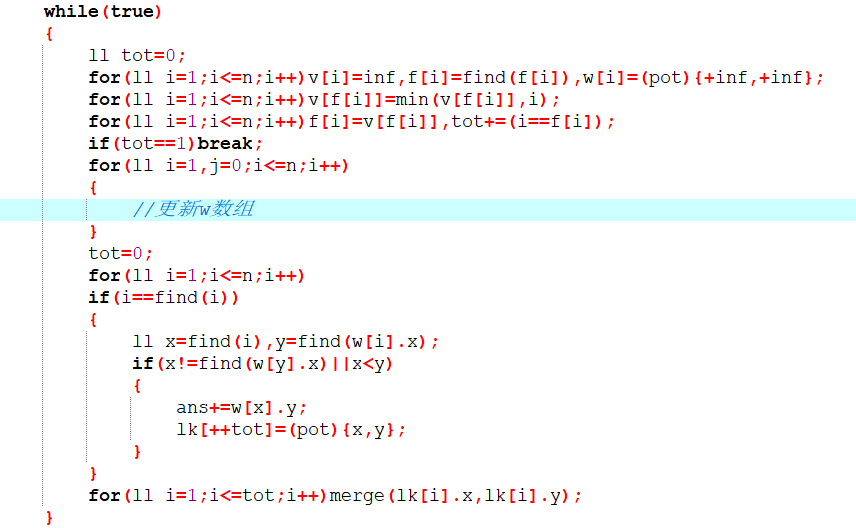
1.为了避免边权相同的情况，以点标号为第二关键字，为了方便维护最小点编号，把每个联通块在并查集上的代表元素设为该联通块内的最小元素。
2.这个算法执行完后会有重边，可以利用一些奇怪的方法去重。
3.注意把给边去重和merge这两部分操作分开做（防止影响f数组）。