04 详解”死亡ReLU“问题

本篇文章尝试通过具体的神经网络例子，来深入探讨”死亡ReLU“的问题。

很多资料都会提到神经元”永久性死亡“这种说法，我认为这会对我们的理解产生一定的误解。事实上，神经元的状态一直都是动态的，是受到多个因素的影响的。那么是哪些因素在什么样的条件下会导致”死亡ReLU“问题呢？

首先我们回顾一下ReLU函数的图像：

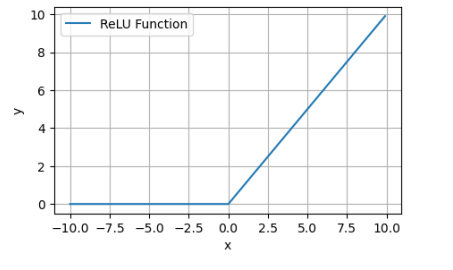
当输入为负时，ReLU函数输出为零。也就是说当输入神经元的加权和为负时，神经元输出为零。此时，神经元进入”失活“状态。

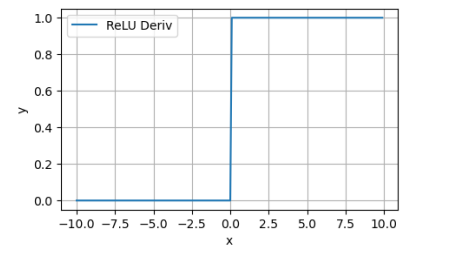
从ReLU的导数图像可知，在这种状态下，ReLU的导数也为0。

我们用一个简单的多层神经网络举例：

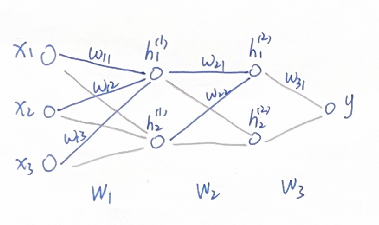
我们用于训练的数据如下，其中每一行为一个sample，共n个samples：

我们分两种情况进行讨论。

情况一

我们把关注点放在第一个中间层的第1个神经元 \(h_1^{(1)}\) ，根据反向传播链式法则，与之相关联的\(w_{11}\) , \(w_{12}\), \(w_{13}\) 的梯度为：

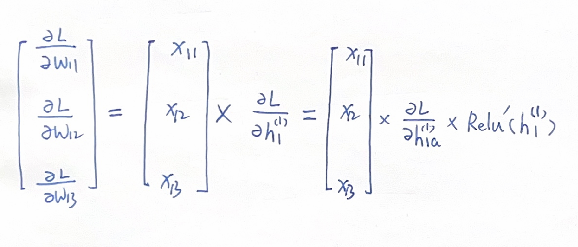
其中 \(h_{1a}^{(1)}\) 表示 \(h_1^{(1)}\) 经过Relu激活函数的输出，\(Relu'(h_1^{(1)})\) 表示Relu函数在 \(h_1^{(1)}\) 处的导数。

此时如果输入神经元的加权和 \(x_{11}w_{11}+x_{12}w_{12}+x_{13}w_{13}\) 小于零，则神经元输出 \(h_{1a}^{(1)}\) 等于0，激活函数导数\(Relu'(h_1^{(1)})\) 等于0，代入上式得到 \(w_{11}\) , \(w_{12}\), \(w_{13}\) 的梯度为0。

而权重的更新公式为：\(w_{11new}=w_{11}-\lambda*\frac{\partial L}{\partial w_{11}}\)

则\(w_{11}\) , \(w_{12}\), \(w_{13}\) 在本次迭代中，没有更新。

请注意，到这里为止，我们不能说神经元”死亡了“，只不过是本次迭代中输出为0，Relu导数为0，导致权重没有更新。（一些网上资料的表述方式会让人产生误解）

如果下一组输入数据 \({x_{21}, x_{22}, x_{23} }\) 进入网络，其加权和大于0，那么神经元的输出大于0，激活函数导数为1， \(w_{11}\) , \(w_{12}\), \(w_{13}\) 是可以得到更新的。

然而如果你十分不幸，当你把数据集里的所有samples都输入网络进行了训练，你所初始化的权重\(w_{11}\) , \(w_{12}\), \(w_{13}\) ，使得他们的加权和都是小于0的， \(w_{11}\) , \(w_{12}\), \(w_{13}\) 都不会得到更新。整个训练过程中，你发现 \(h_1^{(1)}\) 这个神经元都没有输出。此时，我们可以认为该神经元对于本次训练来说是”死亡“的。

也许你重新初始化了一下权重，重新进行训练，它就活过来了。

对于其他中间层的神经元，其原理也是一样的，如果权重设置不当，所有数据集中的samples都使得该神经元的输入为负，那么它相当于是”死亡“的。

情况二

当我们设置的权重更新步长λ太大时，也有可能导致神经元的”失活“。

我们把关注点放在第二个中间层的第1个神经元 \(h_1^{(2)}\) ，与之相关联的\(w_{21}\) , \(w_{22}\)权重更新公式：

\(w_{21new}=w_{21}-\lambda*\frac{\partial L}{\partial w_{21}}\)

\(w_{22new}=w_{22}-\lambda*\frac{\partial L}{\partial w_{22}}\)

许多资料上是这样描述的：”如果λ过大，则\(\lambda*\frac{\partial L}{\partial w_{21}}\)会很大，会使得权重变为负值。然后和输入进行加权又得到负值，导致relu输入负值，进而失活。”

这样的描述假定了权重的梯度是正值，有些简略。我们把\(w_{21}\) , \(w_{22}\)的梯度写出来看一看：

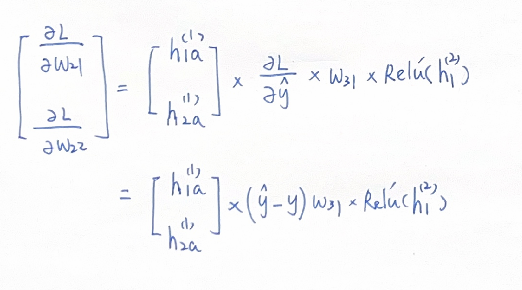
可以看到梯度的正负是与前一层神经元的输出、预测值与实际值大小、后一层与之关联的权重\(w_{31}\)、还有当前神经元激活函数的导数相关联的。

由于前一层神经元也是通过ReLU激活的，那么如果前一层的两个神经元本身就是失活状态， \(h_{1a}^{(1)}\) 和 \(h_{2a}^{(1)}\) 为0，那么\(w_{21}\) , \(w_{22}\)权重不会更新。

如果前一层神经元是激活状态，ReLU函数输出 \(h_{1a}^{(1)}\) 和 \(h_{2a}^{(1)}\) 为正，同时预测值\(\hat{y}\)大于实际值y，同时\(w_{31}\)为正，同时\(w_{21}\) , \(w_{22}\)设置合理， \(h_1^{(2)}\) 这个神经元本身处于激活状态，\(Relu'(h_1^{(2)})\) 为1，那么这种情况下，\(\frac{\partial L}{\partial w_{21}}\), \(\frac{\partial L}{\partial w_{22}}\)为正值。此时，λ过大的话，\(w_{21}\) , \(w_{22}\)会变成负数。在下一次前向传播时，由于前一层无论激活与否都不可能输出负值，因此，与\(w_{21}\) , \(w_{22}\)进行加权，就会导致ReLU的输入为负，神经元失活，\(w_{21}\) , \(w_{22}\)不更新。

这种情况有没有可能在后续的迭代中让神经元重新激活？很遗憾没有，因为前一层也是ReLU函数，其输出不可能是两个负数，从而使他们与\(w_{21}\) , \(w_{22}\)的加权和变为正数。因此\(w_{21}\) , \(w_{22}\)会一直不更新。该神经元相当于”死亡“了。

总结

“死亡ReLU”问题虽然分析起来影响因素较多，看起来十分复杂，但在实际的应用过程中，这种“死亡”并不会对我们的深度神经网络有太大的影响。如果你训练一个神经网络，发现其中有2-4成的神经元都是死亡的，但神经网络依然能够work，这也是正常现象。有一些手段比如Leaky ReLU，ELU等变体能够一定程度上改善“死亡ReLU”问题，但其功效大小在业界也存在一定的争议。更多的情况下，如果你发现大面积“死亡ReLU”问题，重新初始化一下权重矩阵，降低一些优化步长λ，就可以了。